Ladevorgang -
-
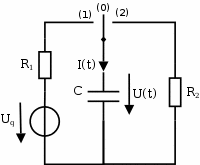 Schaltung zum Auf- Entladen eines Kondensators Nach dem Umschalten des Schalters von Stellung (0) auf (1) gilt für die Spannung U(t): -
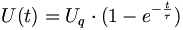 , , (vorausgesetzt, der Kondensator war zu Beginn ungeladen: U(0)=0 V). Im Einschaltmoment stellt der Kondensator einen Kurzschluss dar, deshalb muss ein Kondensator immer über einen Vorwiderstand aufgeladen werden. Es gilt: -
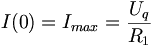
Für die Stromstärke I(t) gilt:
-
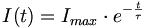
Die Ladezeit des Kondensator ist proportional zur Größe des Vorwiderstandes R und proportional zu seiner Kapazität C. Das Produkt von Vorwiderstand und Kapazität nennt man die Zeitkonstante τ.
-
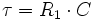
Theoretisch dauert es unendlich lange, bis U(t)=Uq ist. Für praktische Zwecke kann man die Ladezeit tL
-
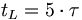
betrachten, nach der der Kondensator näherungsweise als vollständig geladen angesehen werden kann.
Herleitung (Ladevorgang)
Zur Herleitung betrachte man folgendes Schaltbild:
Der Ladestrom I ist zeitabhängig: I=I(t), denn er ergibt sich aus der über dem Widerstand R auftretenden Spannungsdifferenz UB-U(t), wobei U(t) die Spannung ist, auf die der Kondensator zur Zeit t schon geladen ist und UB die Quellenspannung. Somit gilt
-
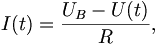
d.h. aufgelöst nach U(t):
-
- U(t) = UB - IR.
Die elektrische Ladung auf dem Kondensator ist
-
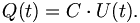
Andererseits ist der Strom die zeitliche Ladungsänderung, also
-
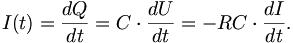
Dies ist eine Differentialgleichung für I(t). Sie wird gelöst durch den Ansatz
-
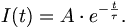
Damit ist nämlich
-
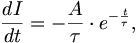
und eingesetzt in die Differentialgleichung
-
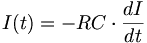
erhält man
-
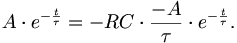
Nach Kürzen von A und der e-Funktion verbleibt
-
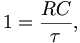
also τ = RC. A ergibt sich aus der Anfangsbedingung
-
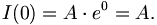
Damit ist
-
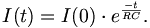
Für die Spannung folgt
-
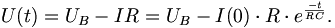
Darin ist
-
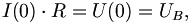
also
-
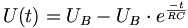
oder
-
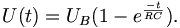
| 
