Blindwiderstand Induktiver Widerstand und kapazitiver Widerstand Induktiver Widerstand und kapazitiver Widerstand sind Blindwiderstände. Sie bewirken eine Phasenverschiebung zwischen Spannung und Strom. Entsprechende (ideale) Bauelemente wandeln keine Energie in Wärme um. In der Praxis haben die Bauelemente aber immer einen Ohmschen Anteil. Der induktive Widerstand einer idealen Spule ist bei Gleichspannung Null und wird mit wachsender Frequenz f bei Wechselspannung größer: 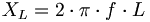 Der kapazitive Widerstand eines idealen Kondensators ist bei Gleichspannung unendlich und sinkt mit wachsender Frequenz f bei Wechselspannung: 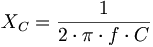 Wenn die Maße eines Bauteils in den Bereich der Wellenlänge kommen, besitzt es sowohl einen nicht zu vernachlässigenden induktiven als auch einen kapazitiven Anteil und wird gegebenenfalls zum Schwingkreis, als Beispiel sei hier die Antenne genannt. Schwingkreis Die Parallel- beziehungsweise Reihenschaltung von Kapazität und Induktivität bezeichnet man als Schwingkreis. Ein Schwingkreis hat einen frequenzabhängigen elektrischen Widerstand. Die Frequenzabhängigkeit des Widerstandes im Schwingkreis, der nur in der Nachbarschaft der Resonanzfrequenz extremal (minimal beziehungsweise maximal) wird. Dieser Effekt wird unter anderem angewendet, um aus einem Gemisch von Signalen unterschiedlicher Frequenz eine bestimmte Frequenz herauszufiltern.
Vergleiche: Der Tiefpass läßt nur tiefe Frequenzen passieren und der Hochpass läßt nur hohe Frequenzen passieren.
Meistens wird jedoch die aktive Filterwirkung eines Tiefpass-Filters (das ja die hohen Frequenzen abschneidet und entfernt) besser beschrieben mit: Höhensperre, Höhenfilter, High Cut, Treble Cut und Rauschfilter und die aktive Filterwirkung eines Hochpass-Filters (das ja die tiefen Frequenzen entfernt) wird eindeutiger und praktischer dargestellt mit: Tiefensperre, Bassfilter, Low Cut, Bass Cut, Trittschallfilter und Rumpelfilter. Beim realen Schwingkreis treten Kondensatorverluste und Spulenverluste durch deren Ohmschen Widerstand auf. Den ohmschen Widerstand des Kondensators kann man aber meist vernachlässigen. Für den Resonanzwiderstand im Parallelschwingkreis ergibt sich: 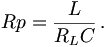
Dieser wird bei der Resonanzfrequenz erreicht, die folgendermaßen berechnet werden kann:
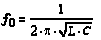
| 
