Erläuterung Iteration
Nullstellen von Funktionen erhält man mit Interationverfahren. Dazu wird in das Feld links der Funktionterm eingegeben.
Beachte
Variable ist x
Funktionen sin, cos, tan, exp, log und sqr (Wurzel) stets mit Klammern
Zwischen Konstanten und Variablen gehört der * : Also 2*x und nicht 2x
Mit dem Button Zeichnen wird die Funktion nach Analyse der Eingabe gezeichnet.
Durch die Buttons x-Maßstab und x-Maßstab wird der Maßstab in x bzw y-Richtung halbiert, sodaß nun mehr zu sehen ist.
Ausschnitte erhält man, wenn man mit der Maus um eine Nullstelle ein Rechteck zieht.
Newtonverfahren
Mit dem Button Newton-Iter. beginnt das Newton Verfahren.
Zunächst wird mit der Maus ein Startwert in der Nähe der Nullstelle bestimmt.Mit dem Button Iter.-Schritt wird dann zu jedem Wert xn der folgende Wert xn+1 wie folgt berechnet: Bei xn wird die Tangente konstruiert. Der Schnittpunkt dieser Tangente mit der x-Achse ist xn+1.
Iterationsformel:
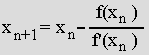
Das Newtonverfahren konvergiert stets sehr schnell gegen die Nullstelle, ist aber nicht narrensicher!
Intervall-Halbierung
Mit dem Button Interv.-Halb, beginnt das Intervall-Halbierungs Verfahren. Verfahren.
Zunächst werden mit der Maus zwei Startwerte rechts und links von der Nullstelle markiert. Mit dem Button Iter.-Schritt startet dann das Verfahren: Zunächst wird die Mitte bestimmt und dann geprüft, in welchem Teilintervall (grün markiert) die Nullstelle liegt.
Dieses Intervall wird nun erneut unterteilt... etc Bei stetigen Funktionen ist dieses Verfahren langsamer als das Newton-Verfahren, dafür narrensicher!
| 
