|
Exponenten und
BasisExponent = Basis * Basis(Exponent-1) für ungerade
Exponenten
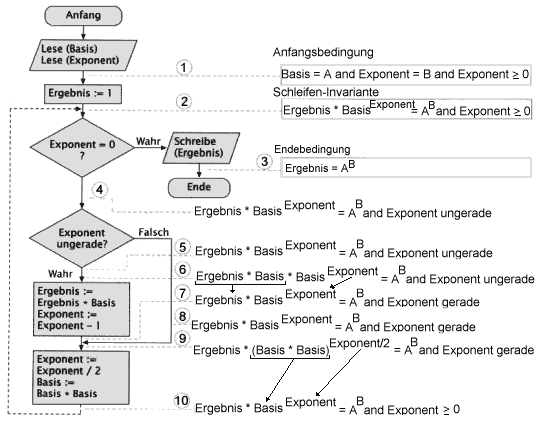
Die Anfangs- und Endebedingung kann sofort hingeschrieben
werden. Nun sind alle Anweisungen und Pfade des
Programmablaufplans durchzugehen und zu zeigen, daß man aus der
Anfangsbedingung durch das Programm die Endebedingung erhält.
Die Schleife möge man sich vorläufig als aufgeschnitten denken.
Die an der Stelle (2) gegebene Zusicherung ist der Angelpunkt des
ganzen Verfahrens. Diese muß zunächst intuitiv gefunden werden
und in geeigneter Weise formuliert werden. Ausgehend von dieser
Behauptung (2) können nun weitere Zusicherungen abgeleitet werden.
Zusicherung (3) ergibt sich aus (2), da Exponent = 0
ist und Basis0 = 1 gilt. (4) folgt unmittelbar
aus (2). Um (7) aus (5) abzuleiten, wird (5) in die äquivalente Form (6)
umgeschrieben. Durch Ersetzen in (6) von Ergebnis * Basis
durch Ergebnis und Exponent-1 durch
Exponent ergibt sich dann (7). Der
Exponent muß in (7) gerade sein! (8) ist interessanterweise
identisch zu (7). (7)/(8) kann in (9) umgeformt werden
( (x*x)(y/2) = x(2*y/2) = xy ).
Durch Ersetzen von Exponent/2 durch Exponent und
Basis * Basis durch Basis in (9) erhält man (10).
Danach ist in (10) der Exponent gerade oder ungerade aber größer
gleich Null. Schließt man nun die Rückwärtsschleife von (10)
nach (2), so sieht man die Übereinstimmung der Zusicherungen (10)
und (2). Damit ist die Schleife widerspruchsfrei geschlossen.
Die Zusicherung (2) gilt offenbar für den ersten Durchlauf der
Schleife, da mit Ergebnis = 1 ,
mit Basis = A und Exponent = B der Ausdruck
Ergebnis*BasisExponent = AB wahr
ist. Aufgrund des geführten Beweises gilt die Zusicherung auch
für den zweiten Durchlauf und allen folgenden Durchläufen.
Damit ist bewiesen, daß das Programm tatsächlich AB liefert,
wenn es das Ende erreicht.
Wird jetzt noch nachgewiesen (nicht hier!) daß das Programm
auch nach endlich vielen Wiederholungen aufhört (terminiert), so
ist die Korrektheit des Programms formal bewiesen und es sind
keine Tests nötig.
Der Aufwand den Verifikationsweg zu beschreiten ist enorm und
wird in ausgesuchten Situationen beschritten. Es gibt
abgewandelte Verfahren w.z.B. das symbolische Testen die öfter
in der Praxis eingesetzt werden. Das Fehlerfinden mittles Testens
mittels Testfälle ist das bisher am häufigsten eingesetzte
Verfahren.
| 
