Digitalisierung von Tönen

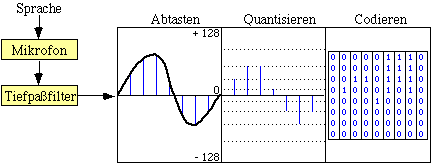Digitalisierung ist ein Prozeßblock, der aus zwei Teilen besteht. Der erste hat die Aufgabe, das aufgezeichnete Material in eine computergerechteForm zu bringen, es wird analog/digital gewandelt (A/D-Wandlung).Das folgende Bild zeigt, wie aus einer analogen Sinuskurve eine Wavetable,d. h. eine Zahlenmenge, wird. Der zweite Teil muß die Ergebnisse der Arbeitdes Computers wieder den menschlichen Sinnen zugänglich machen, und zwardurch den umgekehrten Vorgang, die Digital-Analog-Wandlung (D/A-Wandlung).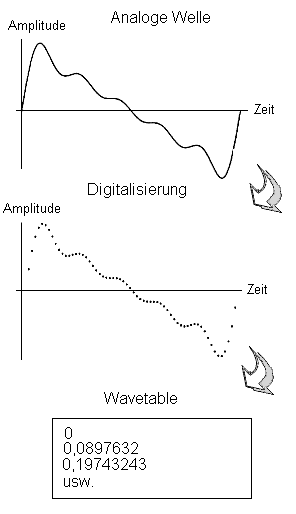

Das entscheidende Charakteristikum der Digitalisierung besteht darin, daß aus einem kontinuierlichen Kurvenzug mit unendlich vielenZwischenwerten eine kleine Menge diskreter Punkte wird. Der analogeTon kann rein theoretisch in unendlich viele Werte zerlegt werden,er ist ein kontinuierliches Signal, das durch den Digitalisierungsvorgangin eine endliche Anzahl von Einzelpunkten aufgelöst wird. Auch wenn eine analoge Schwingung nur die endliche Zeitdauer von einer Sekunde hat, setzt sich diese doch aus unendlich vielen Zeitpunkten zusammen.Die Digitalisierung ändert daher eine wichtige Eigenschaft des analogen Signals, indem sie es aus einem kontinuierlichen undunendlichen in ein diskretes und endliches verwandelt.

Wie läuft so etwas technisch ab? Der Schlüsselbegriff der modernen Digitaltechnik heißt Sampling (sample = Beispiel, Muster). Ein digitalesSignal entsteht dadurch, daß von einem analogen Signal Samples genommen werden. Diese Abtastung geschieht in regelmäßigen Abständen mit hoher Geschwindigkeit, typisch sind 40 bis 50 kHz. Die 'Löcher' der digitalen Welle im Bild oben werden dadurch gefüllt, es entsteht eine treppenförmige Kurve. Der Abstand jedes Punktes von der Null-Linie ist der Digitalwert, der als reiner Zahlenwert gespeichert wird. Mit einer für Soundadapter üblichen Sampling-Rate von 48 KHz sind das 48000 Werte pro Sekunde, die einen entsprechenden Speicherplatzbedarf haben. Ein zweites Kriterium ist die Auflösung eines Samples, d. h. in wieviele Stufen der Spannungsbereich zwischen Null und der maximalen Ampkitude aufgeteilt wird.

Die Digitalisierung führt zu einer Reihe von störenden Nebenwirkungen, die grundsätzlicher Natur sind und durch besondere Maßnahmen beseitigt werden müssen. Sie treten bei der Wiedergabe, d. h. der D/A-Wandlung, auf. Angenommen man hätte pro Welle einer Schwingung nur ein einziges Sample genommen. Dann gibt es bei der D/A-Wandlung mehrere (!) Möglichkeiten, aus diesem eine analoge Schwingung zu rekonstruieren. Da man dann nicht weiß, wo die negative Halbwelle liegt, paßt z. B. auch eine Welle mit halber Frequenz zu diesem Wert. Wir brauchen also mindestens zwei Werte, um eine Schwingung aus Wellenberg und Wellental richtig vermessen zu können. Die folgende Grafik illustriert diese Problematik:

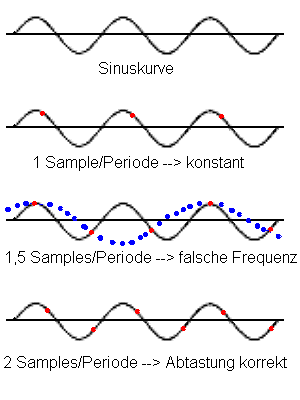
Daraus erklärt sich auch z. B. die bei CD-Spielern verbreitete Sampling-Rate von 44,1 KHz. Da der Mensch Töne bis etwa 20 kHz hören kann, müssen diese mit der doppelten Frequenz abgetastet werden, damit sie eindeutig analysierbar sind. Man kann beweisen, daß bei Erfüllung der beiden folgenden Forderungen keine Informationsverluste entstehen, wenn das digitale Signal wieder in ein analoges zurückverwandelt wird:

1. Die Sampling-Rate muß mindestens doppelt so groß sein wie die höchste zu verarbeitende Frequenz.
2. Das Signal darf keine Frequenzen enthalten, die über der halben Sampling-Rate liegen.

Beide Forderungen folgen aus zwei wichtigen Forschungsergebnissen der Nachrichtentechnik und Informationstheorie. Harry Nyquist formulierte 1928 das Nyquist-Kriterium, nach der man eine Sampling-Frequenz finden kann, mit der es möglich ist, ein digitalisiertes Signal verlustfrei wieder zurückzuverwandeln. Der amerikanische Mathematiker Claude E. Shannon stellte 1949 das Abtasttheorem auf. Es gibt an, wie viele Werte man für eine verlustfreie Rekonstruktion des Ausgangssignals benötigt. Aus technischer Sicht folgt aus allem, daß man unbedingt sicher gehen muß, daß keine höheren, möglicherweise außerhalb des Hörbereichs liegende Frequenzen in dem zu digitalisierenden Signal enthalten sind. Andemfalls treten hörbare Störungen auf, die man als Aliasing (von lat. alias = anders) bezeichnet. Daher wird am Eingang eines A/D-Wandlers ein Tiefpaßfilter eingesetzt, das alle unerwünschten Frequenzen unterdrückt. Die moderne CD-Technik erleichtert dies noch durch Oversampling. Dabei wird das Eingangssignal mit einer sehr hohen Frequenz abgetastet (bis zu 6 MHz), die die Filterung verbessert, wonach dann die erhaltenen Werte auf die eigentliche Sampling-Frequenz (z. B. 48 kHz) heruntergerechnet werden.

Zur Wiedergabe wird umgekehrt ein Digital-Analog-Umsetzer verwendet, der die digitalisierten Wellenformen wieder in analoge Spannungsschwankungen umsetzt. Danach kann über einen Verstärker und Lautsprecher die Umsetzung in akustische Schwingungen erfolgen. Die 'Lücken' bzw. 'Treppen' eines digitalen Signals müssen wieder durch ein Filter beseitigt werden. Auch hier hilft Oversampling bei der Unterdrückung von Störungen, u. a. bei der Reduzierung von Quantisierungsrauschen, das während des Digitalisierungsprozesses entsteht.
Die Manipulation der Abtastrate ermöglicht aber auch typische Sampler-Effekte. Wird etwa das Sample bei der Wiedergabe mit einer anderen Abtastrate als bei der Aufnahme abgespielt, ändert sich die Tonhöhe.

Hardware zur Aufnahme und Wiedergabe von Tönen

• Sinus-, Dreieck- und Rechteckwellen unterschiedlicher Frequenz,
• Rauschen,
• und gefilterte Komponenten aus den beiden o. a. Komponenten.

Mit der Wavetable-Synthese wird eine Kompromißlösung beschrieben. Hier werden die Klangformen digital abgespeichert und nur die Tonhöhe und Dauer programmiert. Damit lassen sich natürlich klingende Instrumente erzeugen ohne zuviel Speicher zu belegen.

Will man noch mehr Flexibilität, so kann die gesamte Wellenform digitalisiert werden. Damit lassen sich dann auch Sprache und Geräusche auf dem Rechner wiedergeben. Zur Aufnahme wird ein Analog-Digital-Umsetzer verwendet, der die vom Mikrofon, oder der Audio-Quelle stammenden analogen Signale in digitale Werte umwandelt.

Soundkarten erlauben meist unterschiedliche Werte für die Abtastrate: 11 kHz, 22 kHz, 44 kHz und 48 kHz oder stufenlose Einstellung. Um den Alias-Effekt bei niederen Abtastraten zu vermeiden, ist meist ein Filter vorhanden, der höhere Frequenzanteile unterdrückt, also werden beispielsweise bei einer Abtastrate von 11 kHz Frequenzen die höher als 5.5 kHz sind unterdrückt.

Wenn man Stereo-Sound ausgeben will, so benötigt man für jeden Kanal eine Wave-Datei. Die Wave-Dateien benötigen der Abtastrate entsprechend viel Speicherplatz. Bei 22 kHz sind das entsprechend 22000 kByte pro Sekunde Audio. Die Werte liegen bei den Soundkarten im übrigen nicht genau bei 11 kHz, 22 kHz oder 44 kHz, sondern es sind 11025 Hz, 22050 Hz und 44100 Hz.

Diese Werte kommen nicht von ungefähr, sondern sind typische Werte aus dem täglichen Leben. Dazu ein paar Beispiele:

Qualität	Abtastrate [kHz]	Auflösung [bit]	Mono/Stereo	Datenrate [KByte/s]
Telefon	8	8	Mono	8
AM Radio	11	8	Mono	11
FM Radio	22	16	Stereo	88
CD	44	16	Stereo	176
DAT	48	16	Stereo	192

Zurück

Inhaltsverzeichnis

Nächste

Diplomarbeiten zum Runterladen: