 |
Klang- und Tonerzeugung
Zunächst wollen wir uns mit der Erzeugung von Klängen beschäftigen.
Künstliche Töne oder Klänge werden ja dadurch erzeugt, daßdie Membran eines Lautsprechers durch elektrische Signale in Schwingungversetzt wird. Je nachdem, wie oft in der Sekunde die Polarität desStroms durch die Magnetspule des Lautsprechers wechselt, hören wireinen tiefen (wenige Wechsel) oder einen hohen Ton ( viele Wechsel). DieHöhe eines Tons (= Frequenz) wird in Hertz (= Schwingungen pro Sekunde)angegeben. Ausgegangen wird dabei zuerst immer von Sinusschwingungen. Man kann eine Sinusschwingung durch folgende Gleicung beschreiben: f(t) = a*sin(2*PI*f*t) Wie man sieht, hat die Funktion nur zwei Parameter, die sich variieren lassen: Die Amplitude a (= Lautstärke, gemessen in dB) und und dieFrequenz f (= 1/Wellenlänge = Tonhöhe). Eine einfache Sinusschwingung gibt somit einen recht langweiligen Ton.
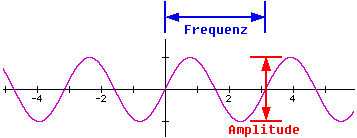
Um unterschiedliche Klangfarben zu erzeugen, muß man verschiedeneWellenformen wählen und diese Wellenformen miteinander mischen. Bezeichnetwird die Wellenform nach Ihrem Aussehen auf dem Bildschirm eines Oszilloskops.Die "reinste" Form ist die oben erwähnte Sinuslinie. EineDreieckschwingung klingt schon härter. Sie wird folgendermaßen aus Sinusschwingungen zusammengesetzt: 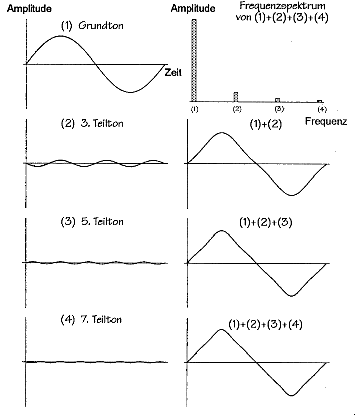 Die Rechteckschwingung (praktisch das Ein- und Ausschalten des Stroms) hatden schärfsten Klang. Sie entsteht ebenfalls aus einem Gemisch von Sinusschwingungen:
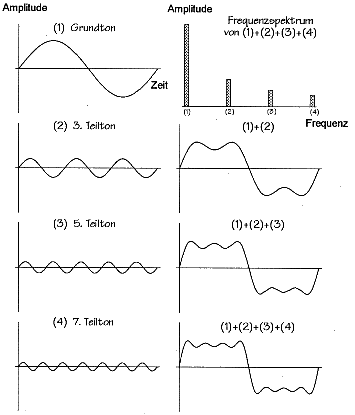
Durch Überlagern und Mischen von unterschiedlichen Schwingungsformen von
verschiedener Frequenz entstehen dann ganz charakteristische Klänge. Die
Erzeugung dieser Töne faßt man unter dem Begriff 'Klangsynthese'
zusammen.
Fourier: Jede Schwingung kann als Summe von Sinusschwingungen
dargestellt werden:
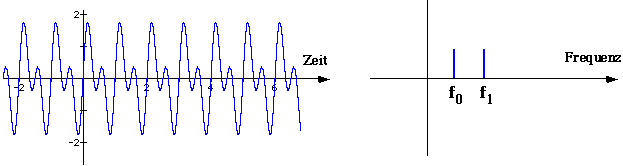
Lineare Synthese
In der Elektronik gibt es zwei grundsätzliche Methoden, um die Erzeugung von Klängen
aus Teiltongemischen technisch zu verwirklichen. Bei der additiven Klangerzeugung
werden Sinustöne gemischt, bei der subtraktiven Sinustöne aus einem Klanggemisch
ausgefiltert. Beides sind Verfahren der linearen Synthese, in der ein geradliniger
Zusammenhang zwischen Eingabe und Ausgabe besteht.
_brigens werden auch Farben mit additiven und subtraktiven Verfahren erzeugt,
denn von der mathematischen Theorie her besteht in dieser Hinsicht kein
wesentlicher Unterschied zwischen Licht- und Tonschwingungen. Etwas von dieser
Gemeinsamkeit kommt darin zum Ausdruck, daß Musiker ebenso gern von 'Klangfarben'
wie Maler von 'Farbtönen' sprechen.
Es kommt bei einem System, das mit der additiven Synthese arbeitet, nur das heraus,
das man vorher hineingetan hat. Heißt z. B. eine Eingabe a, bei der das
Ergebnis a' lautet, und eine andere b mit dem Ergebnis b',
dann erhält man bei Eingabe von a+b das Ergebnis a'+b'. Man
spricht von einem linearen System, und auch die subtraktive Synthese verhält
sich in dieser Weise linear.
Die nichtlinearen Systeme der Klangsynthese zeichnen sich hingegen dadurch
aus, daß sie Frequenzen erzeugen, deren Komponenten man vorher nicht 'direkt'
eingegeben hatte.
Der additiven Synthese liegt die Idee zugrunde, komplexe Schwingungen durch
Addition von einfachen zu erhalten, wie es die Fourier-Methode ermöglicht. Sie
heißt daher auch Fourier-Synthese. Als Ausgangspunkt dienen Sinusschwingungen,
die im richtigen Mischungsverhältnis, d.h. mit passender Tonhöhe und Lautstärke,
gleichzeitig erklingen. Dadurch entstehen die oben beschriebenen Wellenformen
(Dreieck-, Sägezahn- oder Rechtecksschwingungen).
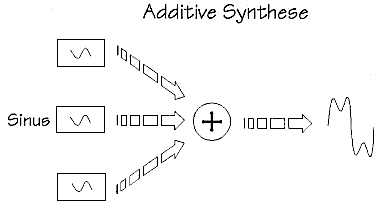
Die additive Synthese spielte besonders in frühen elektronischen Instrumenten
wie der Hammond-Orgel eine wichtige Rolle. Bei den Konstrukteuren digitaler
Computer ist die additive Synthese wegen ihres hohen Rechenaufwandes wenig
beliebt. Eine weitere sehr interessante Anwendung ist das Erzeugen akustischer
Illusionen. Man kann Töne synthetisieren, die die Illusion erzeugen, ständig
höher zu werden, ohne jemals den Hörbereich zu verlassen (Shepard-Effekt).
Führt bei der additiven Analyse der Syntheseweg von einfachen Klanggemischen
zu Komplizierten, so ist es bei der subtraktiven Synthese gerade umgekehrt.
Aus einem komplexen Signal, das möglichst viele Teiltöne enthält (z. B. ein
Rechtecksignal), werden die unerwünschten Komponenten ausgefiltert.
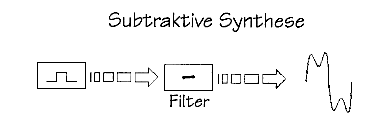
Viele der ersten Synthesizer benutzen diese Anordnung, z. B. die
Moog-Synthesizer. Auch bei Elektroorgeln sind Sägezahnwellen, die (fast)
alle Teiltöne enthalten, oder Rechteckswellen beliebt.
Die subtraktive Synthese ist auch das natürliche Prinzip, nach dem
traditionelle Instrumente wie Flöte, Geige, Klavier usw.
funktionieren, denn bei ihnen wirken Stoff und Form der Resonanzmaterialien
wie Holz, Metall, Darm usw. als natürliche Filter. Resonanz bedeutet, daß auf
Grund der Eigenschaften eines Materials bestimmte Frequenzbereiche besonders
hervorgehoben werden.
Ausgeprägte Resonanzen über feste Frequenzbereiche heißen Formantbereiche.
Für den Vokal 'u' liegt ein solcher Bereich beispielweise zwischen 200 und 400 Hz,
beim 'o' von 400 bis 600 Hz und beim 'a' zwischen 800 und 1200 Hz. 'e' und 'i'
haben sogar jeweils zwei Formanten, das 'e' bei 400 bis 600 Hz bzw. 2200 bis
2600 Hz, das 'i' bei 200 bis 400 Hz bzw. 3000 bis 3500 Hz.
Mund- und Zungenstellung wirken dabei wie Filter, die bestimmte Frequenzen
durchlassen oder abschwächen. In der Elektronik kann sich Resonanz so stark
aufschaukeln, daß selbständige Töne entstehen (Selbsterregung). Für solche
Effekte wurden besonders die Filter der Moog-Synthesizer berühmt.
Man baut also mit elektronischen Mitteln natürliche Modelle nach, und das
Basismodell, auf dem die subtraktive Synthese beruht, besteht darin, daß die
Klänge einer irgendwie angeregten Klangquelle einem Resonanzsystem zugeführt
werden.
Kombiniert man additive und subtraktive Synthese, erhät man weitere Variationsmöglichkeiten.
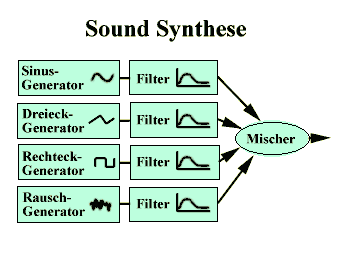
Nichtlineare Synthese
Durch die digitalen Synthesizer wurden ältere, seit dem vorigen Jahrhundert
entwickelte technische Verfahren zur Klangsynthese zwar nicht überflüssig.
Im Gegenteil: auch der digitale Synthesizer machte reichlich von ihnen
Gebrauch. Seine Stärke ist jedoch das Rechnen die neuentwickelten nicht-linearen
Verfahren zur Klangsynthese sind daher mathematische Rechenverfahren, die erst
durch die Digitaltechnik technisch zu realisieren waren.
Zur Erzeugung von Schwingungsformen braucht der digitale Synthesizer
Zahlenwerte. Diese erzeugt er entweder selbst durch Rechenmechanismen, indem er
z. B. die Werte einer Dreiecksschwingung ausrechnet, oder aber er entnimmt sie
einer vorher im Speicher abgelegten Wellentabelle (Wavetable). Diese kann
als Ausgangsmaterial für neue Töne digitalisierte Klänge traditioneller
Instrumente enthalten. Bei der Klangsynthese werden die Wavetables vielfach
verändert und einer nichtlinearen Wellenformung (waveshaping) unterworfen.
Nichtlineare Klangformungsmethoden sind sehr wirksam, weil sie mit relativ
wenig Aufwand sehr komplexe Klänge erzeugen können. Daraus ergeben sich aber
auch Probleme in der Beherrschbarkeit solcher Verfahren. Man will ja nicht
irgendwelche Klänge, sondern musikalisch brauchbare, die sich leicht steuern
lassen, und das ist bei der nichtlinearen Synthese nicht mehr
selbstverständlich. Ihre größten Erfolge haben nichtlineare Methoden bei
komplizierten Glocken und Perkussionsklängen, bei denen auch starke
Geräuschanteile benötigt werden.
FM-Synthese
Um 1973 entwickelte John Chowning, Professor an der amerikanischen
Stanford-Universität, die FM-Synthese (von Frequency Modulation =
Frequenzmodulation). Sie beruht auf Methoden der höheren Mathematik,
die nicht nur Summen und Integrale (wie die Fourier-Analyse) benötigen,
sondern auch bestimmte Formen von Differentialgleichungen (Besselfunktionen).
Chownings Verfahren wurde in unterschiedlicher Form in zahlreichen Synthesizern
der 80er und 90er Jahre eingesetzt.
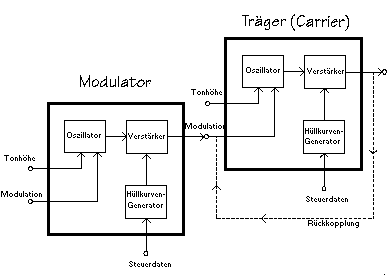
Man verwendet für FM-Synthese im einfachsten Fall zwei Freqenzgeneratoren,
wobei der eine Generator die 'Trägerschwingung', also den eigentlichen Ton,
erzeugt. Der zweite Generator erzeugt die 'Modulatorschwingung', welche die
Trägerschwingung beeinflusst. Das Signal besteht also aus der Addition
beider Schwingungen und folgt dann der (nichtlinearen) Gleichung:
f(t) = a1*sin(2*PI*f1*t + a2*sin(2*PI*f2*t))
Während der Träger direkt mit dem Ausgang verbunden ist, hört
man den Modulator nur in seiner Auswirkung auf den Träger. Die
Veränderungen des Trägers sind durch die Ausgangslautstärke
des Modulators einstellbar. Die Veränderung dieses Ausgangspegels kann durch
eine Hüllkurve erfolgen, wodurch der Ton lebendiger und dynamischer wird.
In der Praxis wird die FM-Synthese noch mit diversen
Rückkopplungsmöglichkeiten verknüpft. Dazu schaltet man den
Ausgang des Trägers zurück auf seinen Modulationseingang, wie dies
im Bild obe durch die gestrichelte Linie angedeutet ist.
Bei einem Klang, zum Beispiel der Ton eines Klaviers, sind aber noch weitere
Parameter zu berücksichtigen. Der wichtigste Parameter ist hier wohl
die Änderung der Lautstärke über die Zeit. Wenn Sie eine
Taste anschlagen, hört nach dem Loslassen der Taste der Ton ja nicht
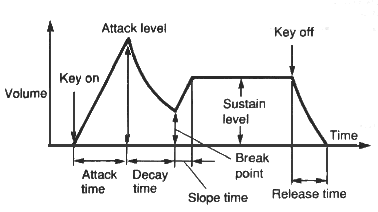
sofort auf, sondern er fällt langsam ab. Man bezeichnet den Verlauf
der Lautstärke als Hüllkurve. Die einzelnen Teile der Hüllkurve
haben alle eine bestimmte Bedeutung. Beim Anschlagen der Taste (Anblasen
einer Flöte, Streichen mit dem Bogen) "Attack" steigt die
Lautstärke von Null auf ihr Maximum, um dann sofort wieder abzufallen
"Decay". Läßt sich der Ton halten ("Sustain")
sinkt die Lautstärke nur auf den Haltewert, um dann nach den Ausschalten
auf Null abzusinken ("Release").
Man kann den Ton nun weiter manipulieren. Durch einen weiteren Generator
mit sehr niedriger Frequenz (LFO) kann man ein Vibrato erzeugen, indem man
die Frequenz des Tons mit dieser Niedrigst-Frequenz (einige Hertz) moduliert.
Hinter die Frequenzerzeugung lassen sich Filter schalten, die den Klang
weiter verändern. Das läßt sich zum Teil sogar ohne jegliche
Hardware rein rechnerisch machen; viele Computer verwenden jedoch bestimmte
integrierte Bausteine für diesen Zweck, sogenannte Soundgeneratoren.
Die von diesen Bausteinen erzeugten Töne klingen je nach dargestelltem
Instrument stärker oder weniger stark "künstlich".
Um die Klänge realer Instrumente naturgetreu wiederzugeben, läßt
sich aber auch eine andere Methode verwenden. Man schließt an den
Computer einen Analog-Digital-Wandler an, der die komplette Wellenform von
Klängen aufzeichnet. Um hier gute Ergebnisse zu erzielen, braucht man
nicht nur Bausteine, die sehr schnell arbeiten, sondern der Computer benötigt
auch einen großen Speicher zur originalgetreuen Aufzeichnung der Klänge.
So aufgezeichnete Instrumente klingen dafür auch sehr realistisch.
Früher hat man solche Klänge nur extern gespeichert (z. B. auf
der Festplatte) und per Abspielprogramm wiedergegeben. Heute bieten auch
die Soundkarten bereits gespeicherte Klänge ('Wavetable-Modul').
|
|
|

