 |
Bildkompressionsverfahren
Bilder mit hoher Auflösung im Computer zu speichern kostet Platz. Bei einerAuflösung von 640 x 480 Bildpunkten und 16 Millionen Farben (24 Bit pro Bildpunkt), benötigt man für ein Bild 921600 Bytes, also fast 1 MByte, Speicherplatz. Bilddateien sind also äußerst unhandlich, besonders dann, wenn ein größeres Bildarchiv angelegt oder ein Farbbild via Modem und Telefonleitung oder per ISDN übertragen werden soll. Daher versucht man Bilder komprimiert abzuspeichern.Erste Schritte zur Verringerung der Dateigröße unternehmen Grafikformate, die intern Kompressionsmethoden wie Lauflängencodierung, LZW- oder Huffman-Codierung verwenden, wie z.B. GIF, PCX oder TIFF. Allerdings überschreiten diese Methoden selbst in ihrer modernsten Form selten den Kompressionsfaktor drei. Jedoch komprimieren diese Verfahren ohne Verluste und das Original läßt sich bis aufs letzte Bit wieder herstellen.
Bei der Reduktion von Bilddaten kann man sogenannte 'Kompressionsverfahren'
verwenden, um die Redundanz in der Bildinformation zu beseitigen. Dabei
unterscheidet man zwischen verlustfreier Kompression, bei der das
unrsprüngliche Bild wieder originalgetreu hergestellt wird und
verlustbehafteter Kompression, wo bei der Kompression ein mehr oder
minder großer Teil der Bildinformation verloren geht.
Ein einfaches Kompressionsverfahren ist die Run-Length-Codierung (RLE).
Dabei verfährt man wie folgt: Das Bild wird z. B. Zeile für Zeile abgespeichert.
Wenn mehrere aufeinanderfolgende Bildpunkte die gleiche Farbe haben, so
speichert man einen Zähler ab, der angibt, wie oft diese Farbe folgt. Der
Zähler ist eine Bildpunktfarbe, die nicht vorkommt und über einen Sonderfall
abgehandelt wird. Dieses Verfahren eignet sich am Besten für Bilder die eine
Palette verwenden und keine Farbverläufe (z.B. bei Fotos) oder komplizierte
Muster enthalten. Bilder in Echtfarben, z.B. von Fotoaufnahmen eignen sich für
dieses Verfahren nicht sehr gut. So lassen sich umgekehrt z.B. Grafiken, die
farbige Flächen enthalten sehr gut mit dem Verfahren abspeichern.
Wenn man komplexere Codierungen z. B. LZW (GIF) verwendet, lassen sich noch
bessere Kompressionsfaktoren erreichen, da dann auch sich wiederholende Muster
erkannt werden. Auch hier gilt, daß Echtfarbenbilder nur schlecht komprimiert
werden können.
Verlustfreie Kompression
Nach dem Satz von Shannon ist die maximale Entropie einer Informationsquelle
S definiert durch
H(S) = Summe(Pi * ld(1/Pi))
wobei Pi die Wahrscheinlichkeit des Auftretens vom Symbol Si ist. ld(1/Pi) ist
der Logarithmus zur Basis 2 von 1/Pi und gibt an, wieviele Bits benötigt
werden, um das Symbol Si zu codieren. Dazu ein Beispiel:
Für ein Bild mit gleichverteilten Graustufenwerten gilt pi = 1/256. Es
werden also 8 Bit benötigt, um jede Graustufe zu codieren. Die Entropie
des Bildes ist 8.
Die folgenden Algorithmen können mit einem einfachen Beispiel erläutert
werden. Es sei die folgende Häfigkeitsverteilung gegeben:
Symbol A B C D E
---------------------------------
Anzahl 15 7 6 6 5
Ein erster Ansatz
Wenn man einen Code mit fester Wortlänge verwendet, benötigt man
3 bit pro Symbol. Für die oben angegeben Anzahlen gibt das
(15 + 7 + 6 + 6 + 5)*3 = 39*3 = 117 bit
Es wird nun versucht, für die häufigsten Symbole einen kurzen, für die
seltenen Modelle einen längeren Code zu finden. Dabei muß auf jeden
Fall die Fano-Bedingung erfüt sein: Kein Codewort eines Codes mit variabler
Wortlänge darf Anfang eines anderen Codewortes sein.
Nun benötigt man nur noch
15*1 + 7*2 + 6*2 + 6*3 + 5*3 = 15 + 14 + 12 + 18 + 15 = 74 bit
Mit zunehmender Zahl von Symbolen würde bei diesem Ansatz die Länge
der Codeworte rasch steigen. Deshalb werden in der Praxis andere Algorithmen
verwendet.
Der Shannon-Fano-Algorithmus
Der Algorithmus hat einen Top-Down-Ansatz:
- Sortiere die Symbole nach ihrer Auftretenshäufigkeit, z. B. ABCDE
- Teile die Folge rekursiv in jeweils zwei Teile, wobei in jeder Hälfte
die Summe der Anzahlen etwa gleich sein sollte. Linke Zweige erhalten die '0'
und rechte Zweige die '1'.
Das sieht für unser Beispiel dann so aus:
/\
0/ \1
/ \
AB CDE
/\
0/ \1
/ \
/\ 0/\1
0/ \1 / \
A B C DE
/\
0/ \1
/ \
/\ 0/\1
0/ \1 / \
A B C /\
0/ \1
D E
Es ergibt sich somit folgende Codierung:
| Symbol | Anzahl | ld(1/p) | Code | Anzahl Bits |
|---|
| A | 15 | 1.38 | 00 | 30 |
| B | 7 | 2.48 | 01 | 14 |
| C | 6 | 2.70 | 10 | 12 |
| D | 6 | 2.70 | 110 | 18 |
| E | 5 | 2.96 | 111 | 15 |
Huffman-Codierung
Dieser Algorithmus verfolgt einen Bottom-Up-Ansatz:
- Init: Trage alle Knoten in eine OPEN-Liste ein, immer sortiert. Z. B: ABCDE.
- Wiederhole, bis die OPEN-Liste nur noch einen Knoten enthält:
- Nimm die beiden Knoten mit der geringsten Häufigkeit (bzw. Wahrscheinlichkeit)
aus der OPEN-Liste und erzeuge einen Eltern-Knoten für sie.
- Weise dem neuen Knoten die Summe der Häufigkeiten (bzw. Wahrscheinlichkeiten)
seiner beiden Kinder zu und trage ihn in der OPEN-Liste ein.
- Weise den beiden Zweigen zu den Kind-Knoten die Werte '0' und '1' zu und
lösche sie aus der OPEN-Liste.
P4(39)
/\
0/ \1
/ \
/ \
/ \
A(15) \P3(24)
/\
0/ \1
/ \
P2(13)/ \P1(11)
/| /\
0/ |1 0/ \1
/ | / \
/ | / \
B(7) C(6) D(6) E(5)
Es ergibt sich somit folgende Codierung:
| Symbol | Anzahl | ld/1/p) | Code | Anzahl Bits |
|---|
| A | 15 | 1.38 | 0 | 15 |
| B | 7 | 2.48 | 100 | 21 |
| C | 6 | 2.70 | 101 | 18 |
| D | 6 | 2.70 | 110 | 18 |
| E | 5 | 2.96 | 111 | 15 |
Für beide Algorithmen gilt:
- Die Decodierung für die beiden Algorithmen ist einfach, sofern
die Codierungstabelle vor den Daten übertragen bzw. mit den Daten gespeichert
wird.
- Kein Codewort ist Beginn eines anderen, die Codierung ist eindeutig (Fano-Bedingung)
und einfach zu decodieren (alle Codesymbole sind Blattknoten des Codebaums).
- Wenn Statistiken über die Daten existieren, liefert die Huffman-Codierung
sehr kompakte Daten.
- Wird eine Standard-Codetabelle verwendet ist die Kompressionsrate geringer,
aber es wird immer noch eine brauchbare Kompression erzielt (z. B. bei Fax, Gruppe 3).
Verlustbehaftete Kompression
Verfahren wie LZW arbeiten verlustfrei, das bedeutet, man erhält nach
der Dekompression exakt das gleiche Bild wie vor der Kompression. Es gibt aber
auch verlustbehaftete Verfahren, die dann stärkere Kompressionsfaktoren
erlauben. Ein Beispiel dafür ist das JPEG-Verfahren, benannt nach der 'Joint
Photographic Expert Group'.
Man erkannte schnell, daß die Bildinformation nicht immer 1:1
erhalten bleiben muß, damit das rekonstruierte Bild sich auf den ersten
Blick nicht vom Original unterscheidet, da schon das Scannen
Farbübergänge in ein Raster preßt (quantisieren). Dies
führte zur Entwicklung eines leistungsfähigeren Verfahrens namens
JPEG durch die gleichnamige ISO/CCITT Kommission.
Der Begriff Verlust ist hier etwas irreführend: es geht nicht
hauptsächlich Bildqualität verloren, sondern Information, die
bis zu einem gewissen Grad redundant ist. So sind mit JPEG Kompressionsraten
von 20:1 möglich, ohne daß man große Unterschiede zum Originalbild
erkennen kann. Das Bild wird dazu in Quadrate von acht Pixeln Kantenlänge
zerlegt und dann mit mathematischen Operationen (Cosinus-Transformation)
komprimiert. Der Kompressionfaktor beeinflußt die Größe der
Datei und auch die Qualität der Wiedergabe. Bei zu hoher Kompression
werden die 8 x 8-Quadrate sogar sichtbar.
JPEG bezeichnet also kein Dateiformat, sondern eine ganze Familie von Algorithmen
zur Kompression digitalisierter Standbilder in Echtfarbqualität.
Diese Sammlung unterschiedlichster Verfahren wurde 1993 unter der Bezeichnung
ISO 10918 als Standard festgeschrieben.
Aus diesem Werkzeugkasten können sich Entwickler je nach gewünschtem
Anwendungsgebiet die benötigten Teile herausnehmen und in ihren Hard-
und Softwareprodukten implementieren.
Dabei kann der Anwender die Kompressionsparameter seinen Anforderungen
entsprechend angeben; dabei sinkt natürlich die Qualität des
komprimierten Bildes mit steigender Kompressionsrate. So können extrem
kleine Bilddateien erzeugt werden, z.B. für Indexarchive von
Bilddatenbanken.
Die verlustbehafteten JPEG-Prozesse sind auf fotografische Aufnahmen mit
fließenden Farbübergängen hin optimiert. Für andere Arten
von Bildern sind sie weniger geeignet z. B. für Bilddaten mit harten
Kontrasten wie Cartoons, Liniengrafiken oder Texte, die meist große
Farbflächen und abrupte Farbwechsel enthalten.
Bei der Entwicklung des JPEG - Standards war es oberstes Ziel einheitliche
Verfahren bereitzustellen, die möglichst alle Belange der
Bilddatenkompression abdeckt. Dabei wurde auf folgende Aspekte besonderen
Wert gelegt:
- Verfahren zur Kompression ohne Datenverlust
- Verfahren zur Kompression mit Datenverlust, allerdings mit einstellbarer
Kompressionsrate
- Algorithmen sollten eine vertretbare Komplexität aufweisen
- Das Verfahren sollte für alle Arten von unbewegten Bilddaten
anwendbar sein, also auch keine Beschränkung der Farbtiefe.
Die verwendeten Algorithmen sollten sowohl in Software als auch in Hardware
relativ schnell und einfach zu implementieren sein.
Untersuchungen des JPEG-Gremiums haben ergeben, daß bei den verlustbehafteten
Umformungsmethoden die 8 x 8 diskrete Kosinustransformation (DCT) die besten
Ergebnisse liefert. Für die Operationen, die auf der DCT beruhen wurde ein
Minimal-Algorithmus, der Baseline Codec festgelegt, auf den alle
DCT-Modi aufbauen.
Die Komprimierung mit dem JPEG Baseline Codec besteht im wesentlichen
aus 5 Schritten:
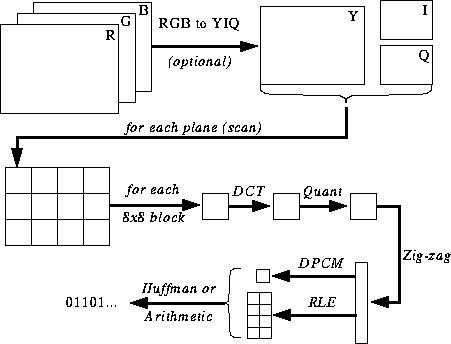
- Konvertierung des Bildes in den YCbCr-Farbraum
- Diskrete Kosinustransformation (DCT)
- Quantisieren der DCT-Koeffizienten
- Codieren der Koeffizienten
- Kompression der Daten
DerYCbCr-Farbraum
Es gibt - wie weiter vorne erwähnt - aber auch Farbmodelle, die
eine Farbe nicht durch die Grundfarben (RGB),
sondern durch andere Eigenschaften ausdrücken. So zum Beispiel das
Helligkeit-Farbigkeit-Modell. Hier sind die Kriterien die Grundhelligkeit der
Farbe, die Farbe mit dem größten Anteil (Rot, Grün oder Blau)
und die Sättigkeit der Farbe, z.B. pastell, stark, fast weiß, usw.
Dieses Farbmodell beruht auf der Fähigkeit des Auges geringe
Helligkeitsunterschiede besser zu erkennen als kleine Farbunterschiede. So
ist ein grau auf schwarz geschriebener Text sehr gut zu lesen, ein blau auf
rot geschriebener, bei gleicher Grundhelligkeit der Farben, allerdings sehr
schlecht. Solche Farbmodelle nennt man Helligkeit-Farbigkeit-Modelle.
Das YCbCr-Modell ist ein solches Helligkeit-Farbigkeit-Modell. Dabei wird ein
RGB-Farbwert in eine Grundhelligkeit Y und zwei Komponenten Cb und Cr aufgeteilt,
wobei Cb ein Maß für die Abweichung von der 'Mittelfarbe' Grau in
Richtung Blau darstellt. Cr ist die entsprechende Maßzahl für Differenz
zu Rot. Diese Darstellung verwendet die Besonderheit des Auges, für
grünes Licht besonders empfindlich zu sein. Daher steckt die meiste
Information in der Grundhelligkeit Y, und man braucht nur noch Abweichungen
nach Rot und Blau darzustellen.
Um nun Farbwerte in RGB-Darstellung in den YCbCr-Farbraum umzurechnen,
benötigt man folgende Formel:
Y = 0,2990*R + 0,5870*G + 0,1140*B
Cb = -0,1687*R - 0,3313*G + 0,5000*B
Cr = 0,5000*R - 0,4187*G - 0,0813*B
Die Rücktransformation vom YcbCr-Farbraum in RGB-Werte geschieht wie folgt:
R = 1,0*Y + 0,0 *Cb + 1,402 *Cr
G = 1,0*Y - 0,34414*Cb - 0,71414*Cr
B = 1,0*Y + 1,7720 *Cb + 0,0 *Cr
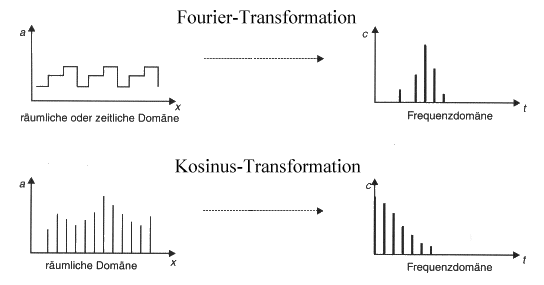
Diskrete Kosinustransformation (DCT)
Das menschliche Auge ist kein perfektes Organ. So kann es zum Beispiel weiche
Farbübergänge viel schlechter auflösen als geringe
Helligkeitsunterschiede. Dabei spricht man bei Farbunterschieden, die das Auge
besser auflöst von niedrigen Ortsfrequenzen, bei schlechterer Auflösung
von hohen Ortsfrequenzen. Die Analogie zu Frequenzen führt von dem
räumlichen Auflösungsvermögen des Auges her. Bei bestimmten
Farbunterschieden kann man mehr unterscheidbare Farbinformationen unterbringen
(daher hohe Ortsfrequenz) als bei anderen Farbunterschieden.
Die DCT nutzt nun diese Schwäche des menschlichen Auges aus, indem sie die
hohen Ortsfrequenzen herausfiltert und diese schlechter oder auch gar nicht
codiert.
Zunächst werden die Eingangsdaten, die als vorzeichenlose Ganzzahlen
vorliegen, in eine für die DCT geeignete Wellenform gebracht. Dazu
subtrahiert man einfach von jedem Wert (2 hoch P-1), wobei P die verwendete Genauigkeit
in Bits darstellt. Im Baseline Codec beträgt die Genauigkeit 8 Bit, so
daß der neue Referentzpunt beim Wert 128 liegt.
Dann werden die Bilddaten in Blöcken zu 8x8 Pixeln gerastert. Ein solcher
Block wird nun als Vektor (aus 64 Pixelwerten) eines geeigneten Vektorraums
interpretiert. Die DCT vollzieht nun einen Basiswechsel. F(u,v) ist der DCT-Koeffizient,
f(i,j) der geshiftete Pixelwert.
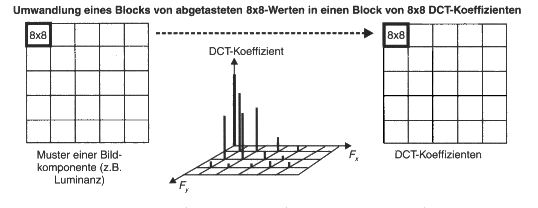
Als Basisvektoren werden aber nun 64 Blöcke zu 8x8 Pixeln verwendet, welche
bezüglich des Vektorraums eine Orthonormalbasis bilden. Die Basisvektoren
gewinnt man durch folgende Formel.
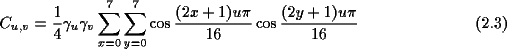
Durch den Basiswechsel ergeben sich 64 eindeutige Koeffizienten, die den Anteil
des jeweiligen Basisblocks an dem Bilddatenblock darstellen. Die Koeffizienten
werden berechnet durch:
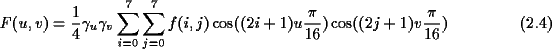
Um diese Koeffizientendarstellung in ihre Ursprungsform zurückzutransformieren,
benötigt man folgende Beziehung:
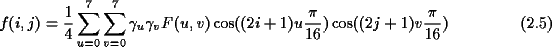
wobei
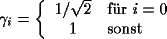
Das folgende Bild zeigt die 8 x 8 = 64 DCT-Basisfunktionen. Links oben
ist F(0,0) (der DC-Anteil), rechts untern der höchste AC-Anteil.

Bei dieser Codierung und Decodierung (Codec) treten schon ohne weitere Behandlung
der Koeffizienten Verluste auf, da die benötigte Kosinus- bzw. Sinusfunktion
nur in begrenzter Genauigkeit auf Rechnern dargestellt werden kann.
Daraus folgt ebenso, daß dieses Verfahren nicht iterierbar ist. Wird also
ein mittels DCT codiertes Bild decodiert und wieder codiert, bekommt man ein
anderes Ergebnis, als bei der ersten Codierung. Der Vorteil der DCT wird bei
Bildern mit kontinuierlichen Farbübergängen besonders deutlich: Da
sich benachbarte Bildpunkte in der Regel kaum unterscheiden, werden in der
Koeffizientendarstellung nur der DC-Koeffizient (das ist der Koeffizient
dessen Basisvektor in beiden Richtungen die Frequenz Null hat) und einige
niederfrequente AC-Koeffizienten (das sind die übrigen Koeffizienten)
größere Werte annehmen. Die anderen sind fast Null oder meistens sogar
gleich Null. Dies bedeutet, daß kleinere Zahlen codiert werden müssen,
und dies hat bei geeigneter Darstellung schon einen Komprimierungseffekt.
Wie man aus den Formeln erkennt, ist die Berechnung der Koeffizienten recht
umfangreich. So benötigt man für einen 8 x 8-Block 63 Additionen und
64 Multiplikationen. Man kann das Problem durch Faktorisierung vereinfachen
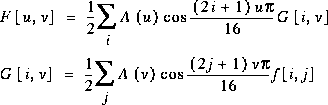
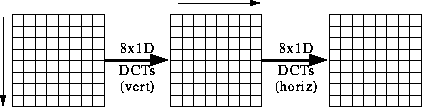
Die meisten Hardware- und Softwareimplementierungen von Coder und Decoder
verwenden Ganzzahlarithmetik und approximieren die Koeffizienten. Die
Multiplikationen reduzieren sich dann auf Schiebeoperationen. Der Weltrekord
für die DCT lag 1989 bei 11 Multiplikationen und 29 Additionen.
Quantisierung
Bei der Entwicklung des JPEG-Standards war es ein Ziel, die Kompressionsparameter
frei wählbar zu machen. Dies wird durch die sogenannte Quantisierung erreicht.
Die Quantisierung ist eine Abbildung, die mehrere benachbarte Werte auf einen neue
n Wert abbildet, wobei die Koeffizienten durch einen Quantisierungsfaktor q(u,v)
geteilt und auf den nächsten Integerwert gerundet werden. Folgende Gleichung
wird dabei verwendet:
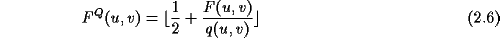
Die Umkehrabbildung multipliziert dann einfach den quantisierten Wert mit dem
Quantisierungsfaktor. Durch diese Hin- und Zurücktransformation entsteht
ein Informationsverlust, da bei dieser Rückrechnung die quantisierten Werte
nicht immer auf den originalen Wert zurückführen. Je größer
dabei der Quantisierungsfaktor ist, desto größer ist auch der
Informationsverlust. Dieser Informationsverlust kann durch geeignete Wahl der
Quantifizierungsfaktoren so gering gehalten werden, daß er vom Auge kaum
wahrgenommen werden kann. Kompressionsraten von < 1:10 sind hierbei leicht
realisierbar, ohne daß beim rekonstruierten Bild große Unterschiede
zum Original zu erkennen sind.
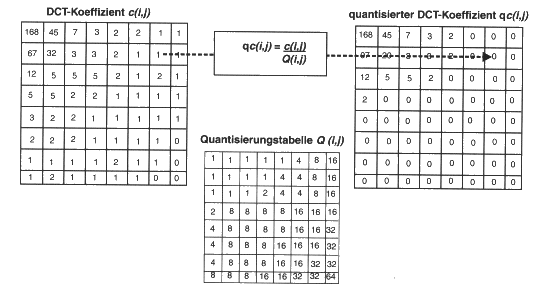
Für die Quantisierung ohne sichtbaren Informationsverlust sind jeweils
für Helligkeit und Farbigkeit optimierte Quantisierungstabellen entwickelt
worden. Diese sind zu entnehmen. In diesen Tabellen werden für den
DC-Koeffizienten und die niederfrequenten AC-Koeffizienten bessere (kleinere)
Quantisierungsfaktoren verwendet als für die höheren Frequenzen. Man
nutzt dabei die oben genannte Schwäche des menschlichen Auges aus.
Tabelle der Quantisierungsfaktoren q(u,v) für die Luminanz
16 11 10 16 24 40 51 61
12 12 14 19 26 58 60 55
14 13 16 24 40 57 69 56
14 17 22 29 51 87 80 62
18 22 37 56 68 109 103 77
24 35 55 64 81 104 113 92
49 64 78 87 103 121 120 101
72 92 95 98 112 100 103 99
Für die Chrominanz wird eine zweite, ähnliche Tabelle verwendet.
Es lassen sich aber auch eigene Tabellen verwenden (die dann im Header der
Bilddatei mitgegeben werden).
Bei Implementierungen von JPEG kann man eine gewünschte Kompressionsrate
(oder Bildqualität) als Parameter einstellen, bei der folgenden Kompression
werden einfach die Quantisierungsfaktoren entsprechend skaliert.
Codierung der Koeffizienten (Zig-zag-Scan)
Die Codierung der quantisierten Koeffizienten erfolgt getrennt für DC- und
AC-Koeffizienten. Aus den 8x8 Blöcken wird ein sequentieller (eindimensionaler)
Bitstrom von 64 Integers erzeugt. Dabei ist der erste Wert der DC-Koeffizient,
allerdings wird nicht der originale Wert, sondern, die Differenz zum
DC-Koeffizienten im vorhergehenden Block codiert. Durch die Kohärenz der
DC-Koeffienten ergeben sich auch hier wieder wesentlich kleinere Zahlen, als
bei der Speicherung der absoluten Werte. Die 63 AC-Koeffizienten werden anhand
einer Zick-Zack-Kurve in sequentielle Reihenfolge gebracht, wodurch eine
Sortierung hin zu höheren Ortsfrequenzen entsteht. Da aber gerade die
hohen Frequenzanteile oft sehr klein bzw. Null sind, entsteht eine für die
weitere Kompression der Bilddaten günstige Reihenfolge.
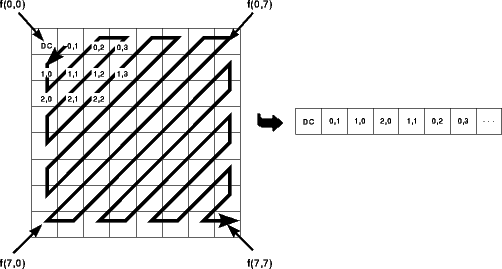
Kompression der Daten
Die bisher beschriebenen Verfahren beinhalten noch keine explizite Kompression,
sondern stellen nur eine, und bei starker Qunatisierung der DCT-Koeffizienten
recht grobe Transformation der Bilddaten dar. Um die so erhaltenen Daten in einem
möglichst kompakten Code abzuspeichern, stellt der JPEG-Standard mehrere
effiziente Verfahren bereit. Diese sind im einzelnen:
- Interne Ganzzahl-Darstellung mit variabler Länge (statt fester Länge)
Der Zahl wird einfach ein Zähler fester Länge vorangestellt, der
angibt, wie lang die nachfolgende Integer-Zahl ist.
- Komprimierung durch Huffman-Algorithmus
Siehe Kompressionsverfahren.
- Arithmetisches Codieren
Das arithmetische Codieren komprimiert zwar besser als das Huffman-Verfahren,
hat jedoch den Nachteil mit verschiedenen Patenten belegt zu sein, so daß
Lizenzgebühren für die Benutzung anfallen. Aus diesem Grund arbeiten
viele Implementierungen mit dem Huffman-Verfahren.
Vergleich JPEG-Codierter Bilder
Das erste Bild ist ca. 28 KByte groß und mit Faktor 1:10 komprimiert.

Das zweite Bild ist nur noch ca. 2,1 KByte groß, der Faktor ist 1:100.

Darstellungsmodi
- Sequential Mode:
Die Bilddaten werden in einem Durchgang, von links oben nach rechts unten codiert.
Besteht ein Bild aus mehreren Komponenten, werden diese nicht nacheinander, also
Komponente für Komponente verschlüsselt, sondern die Komponenten werden
überlappt behandelt. Durch diese überlappte Bearbeitung ist es
müssen nur kleine Puffer bereitgehalten werden, da es möglich ist
die Bilddaten sofort auszugeben, z.B. an parallel arbeitende Prozesse, ohne
warten zu müssen bis alle Komponenten bearbeitet sind. Dieser Modus ist
für die meisten Anwendungen anwendbar, liefert die besten Kompressionsraten
und ist mit am einfachsten zu implementieren.
- Progressive Mode:
Dieser Modus durchläuft das Bild in mehreren Durchgängen, von denen
jeder nur einen Teil der Koeffizienten codiert. Hier bei gibt es wieder zwei
grundlegende Arten: Zum einen können die Koeffizienten in
Frequenzbändern zusammengefaßt und die niedrigen Frequenzen
zuerst verschlüsselt werden, zum anderen werden die Koeffizienten mit
immer besserer Genauigkeit übertragen werden. JPEG erlaubt aber auch diese
Grundarten zu kombinieren, um so bessere Ergebnisse zu erzielen. Schaut man die
Ergebnisse der einzelnen Durchgänge an, so ist das Bild zunächst
unscharf, im Laufe der Übertragung wird es jedoch zunehmend
schärfer. Dieser Mode könnte vor allem bei der
Datenfernübertragung von Bildern eingesetzt werden. Man bekommt
ziemlich schnell einen Überblick auf das übertragene Bild und kann
die Übertragung abbrechen, wenn die Bildqualität ausreichend ist.
- Hierarchical Mode:
Dieser Modus ist eine andere Form des progressive mode. Der hierarchical mode
verwendet eine Menge von Bilder mit immer gröberer Auflösung, die
durch Filtern mit einem Tiefpaß und Mitteln von mehreren Pixelwerten
erzeugt werden. Zunächst wird das Bild mit der kleinsten Auflösung
codiert. Dieses dient wiederum als Basis für eine Vorhersage auf das
Bild mit der nächstgrößeren Auflösung. Dieser Vorgang
wird wiederholt bis die volle Auflösung erreicht ist. Hauptanwendungsgebiet
dürften große Bilddatenbanken sein, die die niedrigeren Auflösungen
für ihre Inhaltsverzeichnisse verwenden und nur bei Bedarf die
höheren Auflösungen decodieren.
|
|
|

