 |
Farbdarstellung
Farbensehen beim MenschenDer Abschnitt über Farbmodelle erklärt zuerst, wie das Farbensehen beim Menschen zustande kommt, bevor auf wichtige Farbmodelle näher eingegangen wird. Im einzelnen sind dies das RGB-Modell, das CMY-Modell und das YIQ-Modell.
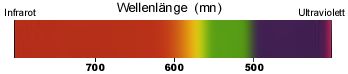
Licht ist elektromagnetische Strahlung und das für den Menschen sichtbareSpektrum ist der Wellenlängenbereich von 400 nm (Violett) bis 700 nm (Rot).
Farben sind ein grundlegender Bestandteil unseres Lebens. Das Farbempfinden
ist bei jedem Menschen unterschiedlich.

Sichtbares Licht ist ein ganz kleiner Teil des Wellenspektrums. Je
nach Länge der Wellen in diesen Spektrum erscheint ein Lichtstrahl
in einer bestimmten Farbe.
Ein Lichtstrahl mit einer Wellenlänge von 700 nm erscheint
rot, ein Lichtrahl mit einer Wellenlänge von ca 500 nm erscheint
blau. So entstehen die Farben.
Wenn ein weißer Lichtstrahl (ein Gemisch aller Wellenlängen)
auf eine Fläche prallt, die alle Wellenlängen außer
Rot absorbiert, dann erscheint diese Fläche rot.
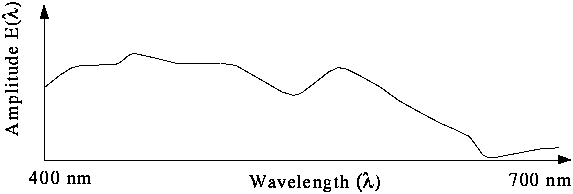
Für das Farbensehen beim Menschen sind bestimmte Sehzellen, die sogenannten
Zapfen zuständig. Es gibt drei verschiedene Sorten von Zapfen in der Netzhaut,
die jeweils mit einem anderen lichtempfindlichen Farbstoff ausgestattet
sind. Ein reines Licht von 400 nm Wellenlänge erregt nur den 'Blaurezeptor'
unter den Zapfen. Ein Licht der Wellenlänge 450 nm erregt den 'Blaurezeptor'
stark und den Grünrezeptor sehr schwach. Licht von 500 nm Wellenlänge spricht
alle drei Zapfensorten an. Die einzelnen Farbeindrücke werden also durch
unterschiedliche Erregungsstärken der einzelnen Zapfensorten ausgelöst.
Gleiche Erregung aller Zapfen führt zum Eindruck ,,weiß``. Es genügen
also drei Grundfarben, um als deren Mischung alle Farben darzustellen.
Betrachtet man Farben nur im Hinblick auf ihren Farbton und nicht auf Helligkeit
und Sättigung, so liegt die Wellenlänge zwischen zwei gerade noch als
unterschiedlich zu erkennende Farben zwischen 2 nm und 10 nm, je nachdem aus
welchem Wellenlängenbereich die Farben stammen. Zur Codierung einer Farbe sind
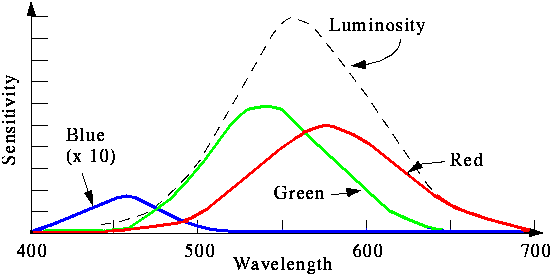
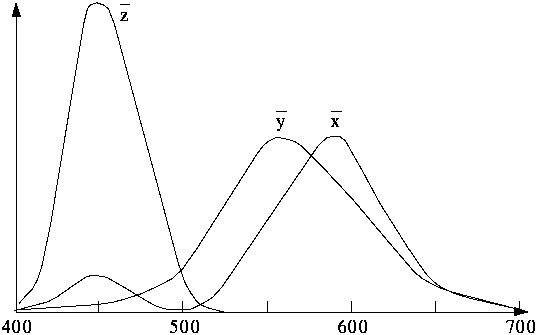
so 3 x 8 = 24 Bit ausreichend. Das folgende Diagramm zeigt die Spektren der
(reinen) Grundfarben, die man addieren kann, um alle sichtbaren Farben darzustellen. Ein
negativer Wert bedeutet dabei, daß die entsprechende Farbe nicht exakt darstellbar
ist.
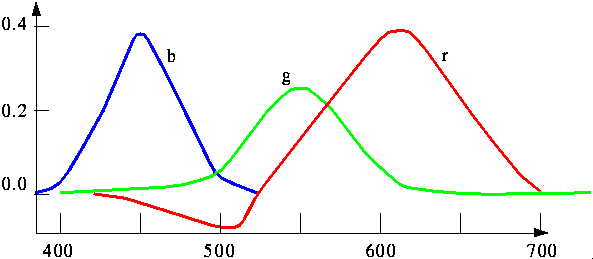
Um alle Farben darstellen zu können, muß man von den Grundfarben abgehen
und 'nicht-reine' Farben verwenden. 1931 definierte die CIE drei Standard-Primärfarben,
(X,Y,Z). Die Primärfarbe Y ist dabei an die Helligkeitsempfindlichkeit des
menschlichen Auges angepaßt
Farb-Kontraste
Farb-Kontraste sind besonders wichtig, wenn mit farbiger
Schrift auf farbigem Hintergrund gearbeitet wird, denn für die Lesbarkeit
des Textes ist nicht allein die Schriftgröße entscheidend.
Grundfarben-Kontrast
Die "klassischen" Grundfarben Blau, Gelb und Rot bilden
untereinander einen starken Farbkontrast. |
 |
Hell-Dunkel-Kontrast
Hier handelt es sich um die gleiche Farbe, jeweils als sehr helle
oder sehr dunkle Nuance. |
 |
Komplementär-Kontrast
Die komplementären Farben liegen sich im Farbkreis gegenüber:
Rot - Grün, Gelb - Lila, Orange - Blau. |
 |
Qualitätskontrast
Farbqualität bedeutet die Intensität einer Farbe
zwischen Reinheit und Trübung. |
 |
Quantitätskontrast
Mengenverhältnis von Farben zueinander (in der Fläche).
|
 |
Simultan-Kontrast
Dieselbe Farbe wirkt auf unterschiedlichem Hintergrund verschieden.
|
 |
Farb-Perspektive
Nicht nur durch Linien, auch mit Farben läßt sich
eine räumliche Wirkung erreichen.
Dominante Farben
Einige Farben drängen sich mehr als andere in den Vordergrund.
Ein Beispiel dafür sind die Signal-Farben Rot oder Orange.
|
 |
| Helle Farben treten in dunkler Umgebung in den Hintergrund. Auf der
anderen Seite treten dunklere Farben vor hellem Hintergrund hervor.
|
 |
Luftperspektive
Man kennt es aus der Natur oder aus Gemäden: wenn man in die Ferne schaut,
wird die Landschaft zum Horizont hin immer bläulicher. Diesen Effekt
kann man ausnutzen, um Tiefe in einem Bild zu erreichen.
|
 |
Farb-Wirkung
Auch auf die Wirkung der Farbwahl auf den Betrachter sollte man achten,
damit das Erscheinungsbild der Webseiten nicht deren Inhalt widerspricht. Seriöse
Firmen meiden beispielsweise knallige Farben. Die Wirkung von Farben ist jedoch kein
allgemeingültiges Gesetz, und wird nicht von jedem Betrachter gleich empfunden.
Langes Lesen ermüdet, Bildschirmarbeit sogar noch mehr. Ziel des Webdesign
soll sein, die Augenbelastung zu vermindern. Die höchste Belastung entsteht
durch weißes Licht. Auch warme Farben belasten uns mehr als kalte Farben.
Am geringsten belasten uns Farben im Bereich Laubgrün bis Gelbgrün.
Farbwahrnehmung erzeugt beim Menschen auch bestimmte psychische Empfindungen:
Warme Farben
Als "warm" gilt die Gelb-Orange-Rot Palette.
- Rot: Aufreizend, beunruhigend, nah; warme Farbtemperaturwirkung
- Gelb: Anregend, nah; sehr warme Temperaturwirkung
Diese Farben werden häufig verwendet, wenn Gefühle ausgedrückt
werden, sie haben eine eher anregende Wirkung.
|
 |
Kalte Farben
Als "kühl" werden Blau-Grün-Töne empfunden.
- Grün: Beruhigend, entfernt; neutrale bis kalte Temperaturwirkung
- Blau: Beruhigend, entfernt; sehr kalte Temperaturwirkung
|
 |
Neutrale Farben
Weiß, Grau und Schwarz wirken am sachlichsten, aber manchmal
auch etwas langweilig. |
 |
Farbmodelle
Man unterscheidet physikalisch-technische und wahrnehmungsorientierte
Farbmodelle. Die wahrnehmungsorientierten Farbmodelle wie z. B. das
HLS-Modell sind mehr auf das Wahrnehmungsempfinden des Menschen
ausgerichtet, das sich eher an den Parametern Farbton (Hue), Helligkeit
(Lightness) und Sättigung (Saturation) orientiert.
Die physikalisch-technischen Farbmodelle beschreiben eine Farbe als Mischung
dreier Primärfarben. Die Unterschiede zwischen den einzelnen Modellen liegen
in der Wahl der Primärfarben und der Art der Farbmischung. Zu den
wichtigsten technischen Farbmodellen zählen:
- RGB-Modell: Ausgabe auf Monitoren
- CMY-Modell: Ausgabe auf Papier
- YIQ-Modell: Fernsehtechnik
Ein Farbmodell soll dazu dienen, Farben anhand einer bestimmten Farbskala zu
beschreiben. Ein Farbmodell kann nicht alle sichtbaren Farben beschreiben,
sondern nur eine Untermenge daraus. Die für die graphische Datenverarbeitung
wichtigeren physikalisch-technischen Farbmodelle sollen nun näher
untersucht werden.
Das RGB-Modell
Das RGB-Modell ist ein additives Farbmodell, d.h. mischt man die drei Farben
Rot, Grün und Blau mit bestimmten Intensitäten zusammen, so ergibt sich
die Farbe Weiß.
Um verschiedene Farben zu mischen, variiert man die Intensitäten
der drei Grundfarben. Mit dem beschriebenen (RGB)-Modell arbeiten
die meisten Bildbearbeitungsprogramme.
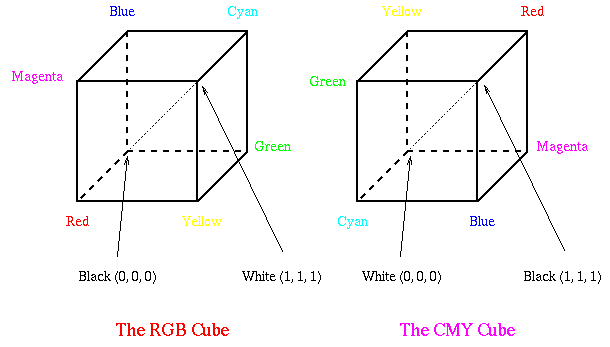
Beim RGB-Modell werden die darstellbaren Farben als Punkte
eines im Ursprung eines Kartesischen Koordinatensystems liegenden
Einheitswürfels beschrieben. Auf den positiven Achsen dieses
Koordinatensystems werden die drei Primärfaben Rot, Grün und Blau
aufgetragen. Die Hauptdiagonale des Einheitswürfels, sie geht vom Punkt
(0,0,0) zum Punkt (1,1,1), enthält die Farben mit gleich großem Anteil an
allen Primärfarben. Sie repräsentiert die Grauwerte, wobei Schwarz im
Ursprung (0,0,0) und Weiß im Punkt (1,1,1) liegen. Eine Farbe wird dann
durch die Anteile an den drei Primärfarben beschrieben, die zur Farbe
Schwarz addiert werden.
Bei Grafikkarten und bei der Farbdefinition für WWW-Anwendungen
wird der reelle Zahlenbereich 0.0 - 1.0 auf den Wertebereich 0 - 255 umgesetzt.
Durch die 256 Werte pro Farbkanal bei drei Kanälen können so 16.7 Mio.
Farben, d. h. Truecolor, festgelegt werden:

Das RGB-Modell ist wichtig bei der Farbdarstellung auf Monitoren. Bei
Farbbildschirmen werden drei Phosphorarten auf der Mattscheibe aufgebracht,
die von drei unabhängigen Elektronenkanonen angesteuert werden und das in
drei Teilbilder (RGB) zerlegte Farbbild erzeugen.
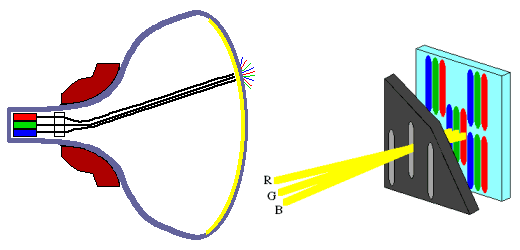
Daraus ergibt sich die
besondere Bedeutung des RGB-Modells: alle anderen Farbbeschreibungen müssen
vor der Farbausgabe in den äquivalenten Punkt des RGB-Würfels umgerechnet
werden.Benutzen zwei Farbbildschirme Kathodenstrahlröhren mit verschiedenem
Phosphor, so ergeben sich auch unterschiedliche Farbskalen. Man kann jedoch
durch eine Transformationsrechnung die auf einer Kathodenstrahlröhre
spezifizierte Farbe auf die Farbskala der anderen Röhre abstimmen.
Das CMY-Modell
Die subtraktive Farbmischung bedient sich der Farben Cyan, Magenta
und Gelb (Yellow). Eine Mischung dieser drei Komponenten ergibt in der Theorie
Schwarz, in der Praxis ein sehr dunkles Braun. Durch Zugabe von Schwarz
(auch Tiefe genannt) enthält man auch im Bereich der unbunten
Farben (Grau, Schwarz, Weiß) eine gute Reproduktionsqualität.
Dieses Modell wird allgemein CMYK genannt.
Bei der Darstellung der Farben in einem kartesischen
Koordinatensystem wie beim RGB-Modell liegt nun Weiß im Ursprung und nicht
mehr Schwarz. Farben werden beschrieben durch die von der Farbe Weiß
abgezogenen Anteile der Grundfarben und nicht mehr durch deren Addition zur
Farbe Schwarz.
Das CMY- oder das CMYK-Modell wird zur Farbausgabe auf Druckern verwendet,
es entspricht dem physikalischen Vorgang der Reflexion weißen Lichts. Die
beim Dreifarbendruck auf das Papier gebrachte Farbe sorgt dafür, daß
bestimmte Farbanteile des Weißen Lichts ausgefiltert und somit nicht mehr
reflektiert werden (s.Abbildung). So verhindert zum Beispiel die auf das Papier
aufgetragenen Farbe Cyan, daß rotes Licht von der Oberfläche absorbiert
wird. Reflektiert wird somit noch der Grün- und Blau-Anteil des Lichts. Die
Druckfarbe Magenta absorbiert Grün und gelbe Druckfarbe absorbiert Blau.
Werden Cyan und Gelb nun übereinander auf das Papier aufgetragen, so wird
nur der Grün-Anteil des anstrahlenden Lichts reflektiert. Werden alle drei
Farben auf das Papier aufgetragen, dann werden Rot, Grün und Blau
absorbiert und man erhält so die Farbe Schwarz.
Die Umrechnung zwischen RGB- und CMY-Modell erfolgt nach folgenden Formeln:
- [C,M,Y] = [1,1,1] - [R,G,B]
- [R,G,B] = [1,1,1] - [C,M,Y]
Beim CMYK-Modell erfolgt die Umrechnung nach folgenden Formeln:
- K = min(C,M,Y)
- C = C - K
- M = M - K
- Y = Y - K
Luminanz und Chrominanz
Hier sollen einige grundlegende Prinzipien der visuellen Empfindung des
Menschen erklärt werden.
Licht sind die durch das Auge vermittelten Empfindungen und elektromagnetischen
Schwingungen einer hestimmten Wellenlänge. Jeder Farbe entspricht eine
andere Wellenlänge. Nicht jede elektromagnetische Schwingung ist sichtbar.
Die für den Menschen sichtbaren Schwingungen bzw. Wellenlängen liegen
im Bereich von etwa 250 nm bis 780 nm.
Eine aus nur einer Wellenlänge bestehende Lichtquelle ist eine monochromatische
Quelle. Nehmen wir als Beispiel an, darf die Wellenlänge dieser monochromatischen
Quelle £ ist. Diese Quelle hat eine Energie, die auch Intensität genannt wird.
Wir nennen diese Intensität C. In Wirklichkeit sind nur wenige Quellen
monochromatisch. Die meisten Quellen setzen sich aus einem Bereich von
Wellenlängen mit je einer eigenen Intensität zusammen. Das ist die spektrale
Verteilung der Lichtquelle, die durch die Funktion C(£) dargestellt wird.
Im sichtbaren Spektrum kann das menschliche Auge zwischen verschiedenen
Wellenlängen monochromatischen Lichts unterscheiden. jede Wellenlänge erzeugt
einen anderen Eindruck, die Farbempfindung.
Die Art, wie das menschliche Auge auf Licht reagiert, weist einige interessante
Aspekte auf, z. B., daß zwei verschiedene Wellenlängen nicht als verschiedene
Farben erscheinen. Zwei monochromatische Quellen mit genau der gleichen
Intensität erwecken einen anderen Eindruck von 'Leuchtdichte'. Das menschliche
Auge reagiert auf bestimmte Wellenlängen empfindlicher als auf andere. Mit
anderen Worten, das Auge reagiert auf manche Farben empfindlicher als auf
andere. Unser Auge reagiert empfindlicher auf Gelb oder Gelbgrün als etwa auf
Rot oder violett.
Die Reaktion des menschlichen Auges V(£) entspricht jeder Wellenlänge
£. Das ist die spektrale Reaktion des menschlichen Sehvermögens.
Die Luminanz einer Lichtquelle oder eines beleuchteten Gegenstands ist kein
physisches Merkmal der Quelle oder des Gegenstands, sondern eine wahrgenommene
Empfindung des menschlichen Betrachters. Luminanz ist ein Produkt der spektralen
Verteilung von Energie durch spektrale Reaktion der menschlichen Sicht.
L = f * C(£) * V(£) * d£
Luminanz ist also ein Maß der allgemeinen Reaktion des Auges auf alle in einer
Quelle oder einem Gegenstand enthaltenen Wellenlängen.
Luminanz und Farbunterschied im analogen Fernsehen
Die drei Signale Rot, Grün und Blau können in drei andere Signale
umgewandelt weren: in die Information der Luminanz (, d. h. die Leuchtdichte
bzw. die Lichtintensität) und zwei weitere Farbsignale.
Das Prinzip der Umwandlung der RGB-Signale in Luminanz- und Farbsignale
ist älter als das Farbfernsehen. Dafür gibt es zwei Gründe. Erstens ist
dadurch eine Abwärtskompatibilität möglich, so daß alte
Schwarzweiß-Fernsehgeräte unterstützt werden. Das ist die Aufgabe des
Luminanzsignals. Da das menschliche Sehvermögen weniger stark auf Farbe
als auf Luminanz reagiert, kann das Farbsignal gegebenenfalls mit geringerer
Genauigkeit übertragen oder dargestellt werden.
In der Fernsehtechnik wird das Luminanzsignal Y-Signal genannt. Die zwei
Chrominanzsignale werden aus den Farbunterschieden herechnet. Ein
Farbunterschiedssignal für Rot, Grün und Blau entsteht durch Suhtrahieren
des Luminanzsignals vom Farbsignal. ist beispielsweise R das Farbsignal
Rot, ist das Farbunterschiedssignal von Rot (R - Y). In der Praxis genügen
zwei Farbunterschiedssignale, wenn Luminanz verfügbar ist.
Farbunterschiedssignale werden nicht so übertragen wie sie sind, sondern
vor der bertragung in zwei Signale - die Cbrominanzsignale - umgewandelt.
Die Umwandlung ist linear. Jede Femsehnorm definiert ihre eigene
Umwandlungsmethode:
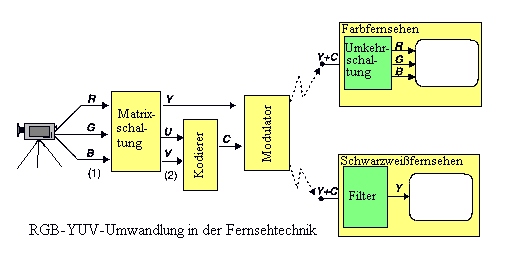
Die NTSC-Norm bezeichnet die Luminanz als Y-Komponente und die zwei
Chrominanzsignale als I- und Q-Komponenten. I und Q bilden zusammen die
Farbton- und Sättigungsaspekte (Chrominanz). Sie werden wie folgt
herechnet:
Y = 0,30*R + 0,59*G + 0,11*B
(1) I = 0,74*(R - Y) - 0,27*(B - Y) = 0,60*R - 0,28*G - 0,32*B
Q = 0,48*(R - Y) + 0,41*(B - Y) = 0,2l*R - 0,52*G + 0,31*B
Die PAL-Norm bezeichnet die Luminanz Y und zwei Chrominanzsignale mit U und V:
Y = 0,30*R + 0,59*G + 0,11*B
(2) U = 0,493*(B - Y) = -0,15*R - 0,29*G + 0,44*B
V = 0,877*(R - Y) = 0,62*R - 0,52*G - 0,10*B
Die folgenden Modelle basieren auf Luminanz und Chrominanz.
Das YIQ-Modell
Das YIQ-Modell wird - wie oben beschrieben - in der Fernsehtechnik verwendet
und sorgt dort für die Abwärtskompatibilität von Farb- zu
S/W-Fernsehen. Die Y-Komponente gibt die Luminanz wieder. Ein S/W-Fernseher
zeigt nur diese Komponente an. Die Chrominanz, die Farbigkeit, ist in den
Komponenten I und Q codiert. Die Umrechnung von RGB-nach YIQ-Werten erfolgt
nach der Formel (1) oben.
Dabei ist I in etwa die Rot-Orange-Achse und Q annähern orthogonal zu I.
Das menschliche Auge ist am Empfindlichsten für Y, danach für I und
schließlich für Q.
Das YCbCr-Farbmodell
Für das PAL-System wurde ein leicht abweichendes Modell entwickelt, das
dann zum CCIR-601-Standard für digitale Videoaufzeichnung wurde. Die
Umrechnung lautet:
- Y = 0,299*R + 0,587*G + 0,114*B
- Cb = B - Y
- Cr = R - Y
Mehr hierzu finden Sie weiter unten beim JPEG-Verfahren.
Daraus leitet sich bei den meisten Bildbearbeitungsprogrammen das HSB-Modell ab.
Es entspricht von allen drei Modellen unserer verbalen
Farbbeschreibung am meisten. Beschreibungen wie ein kräftiges,
helles Gelb lassen sich sofort umsetzen.
Die Initialen stehen für Hue (Farbton), Saturation (Sättigung) und
Brightness (Helligkeit). Der Farbton beeinhaltet die reine Farbinformation,
die Sättigung das Verhätlniss von Stärke der reinen
Farbe und den unbunten Anteilen. Die Helligkeit entspricht der Helligkeit
von 1% - 100%. 0% stellt immer Schwarz dar, 100% immer Weiß.
Zusammenfassung
- Farbbilder werden als Werte-Tripel dargestellt. Man kann durch die
Wahl des Wertebereich unterschidliche Farbtiefe speichern. Für einfache
Icons genügen 2 bis 32 Farben. Bei 8 Bit Farbtiefe wird jedes Pixel
in einem Byte gespeichert und bei 24 Bit Farbtiefe werden 3 Bytes benötigt.
- RGB ist ein additives Farbmodell für selbstleuchtende Geräte
Monitor), CMY ist ein subtraktives Modell für Drucker.
- Bei Video verwendet man YIQ (und YUV, das nicht besprochen wurde).
Y enthält die Helligkeitsinfo (S/W-Bild), I und Q die Farbinfo (Chrominanz).
- Neben diesen Hardware-Modellen gibt es noch andere, die zum Teil auch in
Bildbearbeitungsprogrammen verwendet werden (z. B. HSB).
Gradation
Bei der professionellen Bildbearbeitung
werden fast alls Änderungen an Bildern über sogenannte Gradationskurven
gemacht. Diese Bildberabeitungen sind nötig, um Abbildungen auf
die Besonderheiten spezieller Ausgabegeräte einzustellen oder um
besondere Effekte zu erzielen.
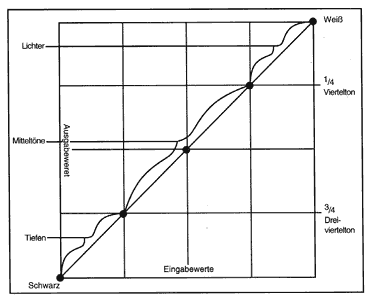
Die Gradationskurve ist die Visualisierung des Verhältnisses
von Eingabe- zu Ausgabewerten in einem Bereich von 0% bis 100%. Diese
Kurve repräsentiert alle Farben eines Bildes, jede Veränderung
ist dort ablesbar. Die Beeinflussung der Farbbereiche eines Bildes durch
die Gradationskurve verdeutlicht die nebenstehende Abbildung.
Gamma-Korrektur
Will man Intensitätsstufen auf einem Bildschirm so darstellen, daß sie gleichmäßig
und ohne sichtbaren Stufen verteilt sind, so muß man spezielle Eigenschaften
des Auges berücksichtigen. Wenn man z. B. 256 Intensitätsstufen linear auf die
Helligkeitswerte des Bildschirms überträgt, so ergibt sich eine nichtlineare Stufung,
die deutlich sichtbar ist. Das menschliche Auge nimmt keine absoluten
Intensitätswerte wahr, sondern Quotienten von Intensitätsstufen.
So wird zum Beispiel zwischen den Intensitätsstufen 0.2 und 0.22 der gleiche
Unterschied wie zwischen 0.6 und 0.66 wahrgenommen. Die Intensitätsstufen
einer Ausgabe müssen daher nichtlinear, genaugenommen logarithmisch auf die
Helligkeitsstufen des Bildschirms abgebildet werden. Für 256 Stufen ergibt sich
dabei folgendes:
- I0 sei die kleinstmögliche Helligkeit und der Wert 1.0 die maximale Helligkeit.
- I0 = I0
- I1 = r * I0
- I2 = r * I1 = r2 * I0
- ...
- I255 = r255*I0 = 1
Der Wert für I0 hängt von der verwendeten Bildröhre ab und liegt normalerweise
zwischen 1/200 und 1/40 des maximal erreichbaren Wertes. Das Verhältnis zwischen
maximaler und minimaler Helligkeit nennt man den Dynamikbereich einer Bildröhre.
Für I0 = 0.02 errechnet sich r = 1.015. Um die Darstellung einer Graustufentreppe
(also Werte zwischen 0 .. 1) ohne Stufen erscheinen lassen ist ein Wert r < 1.01
nötig, dann kann das Auge die einzelnen Helligkeitssprünge nicht mehr
voneinander unterscheiden.
Nun werden die gewünschten Helligkeitswerte durch den Bildschirm auch nichtlinear
verändert, es ist also eine weitere Korrektur notwendig, um eine korrekte
Abbildung zu erreichen.
Die Lichtintensität I die durch einen Elektronenstrahl durch den Phosphor
des Bildschirms umgesetzt wird, hängt von der Zahl der Elektronen N wie
folgt ab:
I = k * N y
Dabei sind k und y Konstanten die vom Bildschirm abhängig sind. y ist der
Wert Gamma und liegt bei den meisten Bildschirmen zwischen 2.2 und 2.5.
Eine Umrechnung der gewünschten Helligkeit auf einen Eingabewert
basierend auf dieser Formel nennt man auch Gammakorrektur.

Mit Hilfe einer Tabelle ist es nun möglich, die gesamte Helligkeits-Korrektur
durchzuführen. Bei manchen Monitoren ist es auch möglich, die Korrekturtabelle
im Monitor abzulegen, üblicherweise wird jedoch die Korrektur in der
Grafikkarte durchgeführt. Natürlich können auch die Bildinformationen selbst
bereits korrigiert werden. Die Korrektur für die Helligkeitsabbildung
kann vorab erfolgen. Insbesondere sind auch Korrekturen für gescannte
Bilder oder Videos nötig, da diese selbst wieder eine andere Helligkeitsumsetzung
aufweisen.
Ähnliche Korrekturen sind auch für Filmbelichter, Drucker etc. notwendig, will
man Bilder mit Graustufen korrekt darstellen. Für eine Korrektur an Farbildern
kann es ggf. nötig sein die Korrektur für alle drei Farbkomponenten getrennt
durchzuführen.
Die folgende Tabelle zeigt typische Werten der Dynamik 1/I0 und der
Anzahl der benötigten Intensitätsstufen. Die Zahl der möglichen
Intensitätsstufen erhält man aufgrund des Dynamik-Bereichs mit der Formel
n = log(1.01(1/I0))
| Technik | Dynamik | Intensitäts-
Stufen |
| Bildschirm | 50 - 200 | 400 - 530 |
| Photo-Druck | 100 | 465 |
| Dia | 1000 | 700 |
S/W-Druck auf
gestrichenem Papier | 100 | 465 |
Farb-Druck auf
gestrichenem Papier | 50 | 500 |
| Zeitung | 10 | 234 |
Dithering
Beachten Sie bitte auch, daß nicht alle Grafikkarten Echtfarben darstellen
können. Bei z. B. VGA oder SVGA, werden die nicht direkt darstellbaren Farben
dann entweder in dem nächstgelegenen anzeigbaren Farbton umgesetzt, wobei
zu nah beieinander liegende Farben gleich erscheinen können, oder diese
Farben werden "gedithert".
Beim Dithering wird ein Farbton durch Kombination vorhandener Farben erzeugt.
Die Kombination besteht darin, daß ein Pixelmuster erzeugt wird, welches
aus einer gewissen Entfernung betrachtet dem gewünschten Farbton ähnelt.
Bei naher Betrachtung sieht man freilich die Pixel. Bei Text kann dieses Raster
aber schnell zur Unleserlichkeit führen.
Möchten Sie sicherstellen, daß ihr Dokument auf nahezu allen Geräten
angezeigt werden kann, so beschränken Sie die Farbe. Es ist sicher heute nicht
mehr nötig, sich auf die 16 Grundfarben zu beschränken. Aber bei der
Farbdefinition von Text- umd Hintergrundfarbe ist es durchaus günstig, sich
auf 256 Farben zurückzuziehen.
Betrachten wir ein Beispiel zum Dithering. Als Ausgangsbild verwenden wir ein
Bild mit Farbverläfen:

Truecolor-Bild
Betrachten wir nun einige Dithermöglichkeiten:

Dithering: optimierte Farbtabelle mit Fehlerdiffusion

Dithering: gleichmäßige Farbtabelle

Dithering: gleichmäßige Farbtabelle mit Fehlerdiffusion

Dithering: Standard-VGA-Tabelle mit Fehlerdiffusion
Sie sehen also, daß auch auf nicht-Truecolor-Systemen erträgliche
Bilder produziert werden können. Ein günstiges Vorgehen ist, auch das
Dithern dem Browser des Betrachters zu überlassen, d. h. Echtfarbenbilder
auch als Echtfarbenbilder zu übertragen. Dennoch sollte man sich als Autor
klar sein, daß ein Bild bei jedem Betrachter gegebenenfalls verändert
erscheint. Man kann sich also nicht darauf verlassen, daß der Betrachter
jedes Detail sehen kann.
Das Beispiel zeigt, daß Dithering auch Übergänge erzeugen kann
(Fehlerdiffusion). Dabei wird versucht, sich der wirklichen Übergang von einer
Farbe über Zwischentöne zur anderen durch ein Muster verfügbarer
Farben anzunähern. Stellt man sich jedoch eine Zeile Text vor, so kann dieser
Effekt zur oben bereits erwähnten Unleserlichkeit führen.
|
|
|

