DIENSTE

	Newsletter abonnieren
	Sag's einem Freund!
	VirtualUniversity als Startseite
	Zu den Favoriten hinzufügen
	Feedback Formular
	e-Learning für Lehrer
	Spenden
	Autoren login

KURSE SUCHEN

Kurse veröffentlichen

Suche nach Datum:

Suche mit Schlüsselwort:

Suche nach Land:

Suche nach Kategorie:



	PARTNER



ausbildung24.ch - Ausbildungsportal, Seminare, Kursen... www.ausbildung24.ch >> HTMLopen.de - Alles was ein Webmaster braucht www.HTMLopen.de >> PCopen.de - PC LAN Netze und Netzwerke - alles was ein IT Profi und Systemtechnicker braucht www.PCopen.de >>

MATHEMATIK

Zurück

Inhaltsverzeichnis

Formelsammlung Algebra

Die Formelsammlung zur Algebra ist ein Teil der Formelsammlung, in der auch Formeln der anderen Fachbereiche zu finden sind.

Inhaltsverzeichnis

1 Grundrechenarten

1.1 Bruchrechnen

2 Klammerersparungsregeln

3 Grundbegriffe der Algebra

4 Grundgesetze

5 Gesetze der Anordnung

6 Betrag Mathematik, Signum, Gaußklammer

7 Termumformungen

8 Grundlegende Funktionen

9 Lineare Gleichungssysteme

10 Quadratische Gleichungen

11 Gleichungen n-ten Grades

12 Polynome n-ten Grades

13 Polynomdivision

14 Horner-Schema

15 Mittelwerte

16 Potenzen

17 Wurzeln

18 Logarithmus

19 Komplexe Zahlen

20 Vollständige Induktion

21 Kombinatorik

21.1 Fakultät
21.2 Binomialkoeffizient („n über k“)
21.3 Binomischer Satz / Pascalsches Dreieck

22 Stirlingsche Näherungsformel

23 Potenzsummen

24 Endliche Reihen

24.1 Rechenregeln
24.2 Arithmetische Reihen
24.3 Geometrische Reihe
24.4 Binomische Reihen

25 Prozentrechnung

26 Zinsrechnung

26.1 Bezeichnungen
26.2 Einfache Zinsrechnung:
26.3 Zinseszins:
26.4 Rentenrechnung
26.5 Rentenrechnung (Nachschüssige Rentenzahlungen)
26.6 Rentenrechnung (Vorschüssige Rentenzahlungen)
26.7 Abschreibung
26.8 Sparkassenformel

Klammerersparungsregeln

Grundbegriffe der Algebra

Grundgesetze

Assoziativ-Gesetz

 a + ( b + c ) = ( a + b ) + c = a + b + c
                                        a · ( b · c ) = ( a · b ) · c = a · b · c

Kommutativ-Gesetz (Vertauschungsgesetz)

 a + b = b + a
                                        a · b = b · a

Distributiv-Gesetz

 a · ( b + c ) = a · b + a · c
                                        a · ( b - c ) = a · b - a · c

Gesetze der Anordnung

Betrag Mathematik, Signum, Gaußklammer

Termumformungen

Grundlegende Funktionen

Quadratische Gleichungen

pq-Formel:

Bringt man die Ausgangsgleichung in die Form

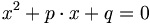
$x^2 + p\cdot x + q = 0$

dann gilt

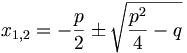
$x_{1,2}= -{p \over 2} \pm \sqrt{{p^2 \over 4} - q}$

abc-Formel: (äquivalent zur pq-Formel)

Bringt man die Ausgangsgleichung in die Form

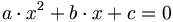
$a\cdot x^2 + b\cdot x + c = 0$

dann gilt

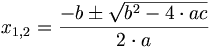
$x_{1,2}=\frac{-b \pm \sqrt{b^2 - 4\cdot ac}}{2\cdot a}$

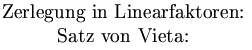
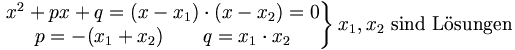
$\left.\begin{matrix} \mbox{Zerlegung in Linearfaktoren:} & x^2+px+q=(x-x_1)\cdot (x-x_2)=0 \\ \mbox{Satz von Vieta:} & p=-(x_1+x_2) \qquad q=x_1\cdot x_2 \end{matrix}\right \} x_1, x_2 \mbox{ sind Lösungen}$

Gleichungen n-ten Grades

Cardanische Formeln Kubische Gleichung

Polynome n-ten Grades

Polynomdivision

Horner-Schema

Mit dem Hornerschema lässt sich die Berechnung von Funktionswerten für ein Polynom vereinfachen. Beispiel:

f (x): = x 2 - 2 x - 8

Dazu legt man eine Tabelle an. Die Anzahl der Zeilen ist drei, die der Spalten um zwei größer als der Grad des Polynoms (für das Beispiel also vier Spalten). Die Koeffizienten scheibt man, von der zweiten Spalte beginnend, in die erste Zeile. Den x-Wert schreibt man in die erste Spalte der zweiten Zeile. Beginnend mit der zweiten Spalte werden die oberen beiden Zahlen addiert. Der Faktor der zweiten Zeile der nächsten Spalte ergibt sich aus der Multiplikation der voranstehenden Summe mit dem x-Wert. Kurz: Senkrecht wird summiert, schräg wird multipliziert. Der Funktionswert befindet sich zum Schluss in der dritten Zeile der letzten Spalte.

Beispiel für $f ( - 2)$ :

      1  -2  -8
                                       x=-2     -2   8
                                       ---------------
                                             1  -4   0

Sollte der Funktionswert, wie hier, Null sein, sind die restlichen Zahlen in der letzten Zeile das Ergebnis der Polynomdivision der Funktion durch $x$ minus den Wert, hier $x - ( - 2)$ : $f (x) = (x - 4)(x + 2)$

Mittelwerte

arithmetisches Mittel von a und b:

${a + b} \over 2$

allgemeiner Ansatz:

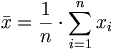
$\bar x = \frac{1}{n}\cdot \sum_{i=1}^n x_i$

geometrisches Mittel von a und b:

$\sqrt{a \cdot b}$

allgemeiner Ansatz:

$\bar x = \sqrt[n]{\prod_{i=1}^n x_i}$

gewogenes arithmetisches Mittel

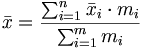
$\bar x=\frac{\sum_{i=1}^n \bar x_i \cdot m_i}{\sum_{i=1}^m m_i}$

Zentralwert

Der Wert, welcher in einer geordneten Liste genau in der Mitte steht, bzw. bei zwei Werten in der Mitte das arithmetische Mittel dieser.

z.B.: 1, 2, 3 -> Zentralwert = 2

z.B.: 1, 2, 3, 4 -> Zentralwert = (2+3)/2 = 2,5

Potenzen

Definition Potenzen

$a^n = a \cdot a \cdot ... \cdot a$ (n Faktoren)

formal:

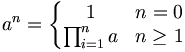
$a^n=\left\{\begin{matrix} 1 & n=0 \\ \prod_{i=1}^n a & n \ge 1 \end{matrix}\right.$

Begriffe zu Potenzen

a n

(das Ergebnis der Rechnung) ist die Potenz

a ist die Basis

n ist der Exponent

Potenzen mit gleicher Basis

$a^x \cdot a^y = a^{x+y}$

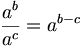
${a^b \over a^c} = a^{b-c}$

Potenzieren einer Potenz

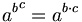
${a^b}^c = a^{b \cdot c}$

Potenzen mit gleichem Exponenten

$x^a \cdot y^a = (x \cdot y)^a$

${x^a \over y^a} = \left( {x \over y} \right)^a$

Wurzeln

Definition Wurzel

$x^n = a \Leftrightarrow x = \sqrt[n]{a}$

Begriffe zu Wurzeln

$x = \sqrt[n]{a}$

n ist der Wurzelexponent

a ist der Radikant

Wurzeln als Potenzen umgeschrieben

$\sqrt[n]{x} = a^{1 \over n}$

Wurzel und Potenz (gilt nur bei ungeradem m und bei geradem m für postive x)

$\sqrt[m]{x ^n} = {\sqrt[m]{x }}\ ^n = x^{n \over m}$

Wurzeln mit gleichem Wurzelexponenten

$\sqrt[n]{a} \cdot \sqrt[n]{b} = \sqrt[n]{a \cdot b}$

${{ \sqrt[n]{a}} \over {\sqrt[n]{b}}} = \sqrt[n]{a \over b}$

Wurzeln aus Wurzel

$\sqrt[n]{{\sqrt[m]{b}}} = \sqrt[n \cdot m]{a}$

Logarithmus

Definition des Logarithmus zur Basis b

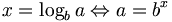
$x = \log_b a \Leftrightarrow a = b^x$

Logarithmus-Gesetze

$\log ( a \cdot b) = \log a + \log b$

$\log \left( {a \over b} \right) = \log a - \log b$

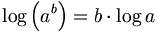
$\log \left( a^b \right) = b \cdot \log a$

Komplexe Zahlen

Vollständige Induktion

Kombinatorik

Fakultät

$n! = 1 \cdot 2 \cdot ... \cdot n = \prod_{i=1}^{n} i$

0! = 1

Binomialkoeffizient („n über k“)

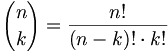
${n \choose k} = \frac{n!}{(n-k)! \cdot k!}$

Binomischer Satz / Pascalsches Dreieck

(a + b) 0 = 1

(a + b) 1 = a + b

(a + b) 2 = a 2 + 2 ab + b 2

(a + b) 3 = a 3 + 3 a 2 b + 3 ab 2 + b 3

(a + b) 4 = a 4 + 4 a 3 b + 6 a 2 b 2 + 4 ab 3 + b 4

...

k = 0... n

$(a+b)^n = {n \choose 0}a^{n}+{n \choose 1}a^{n-1}b+{n \choose 2}a^{n-2}b^2+...+{n \choose n-1}ab^{n-1}+{n \choose n}b^n$

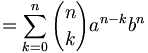
$= \sum_{k=0}^n {n \choose k}a^{n-k} b^n$

Stirlingsche Näherungsformel

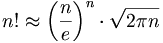
$n! \approx \left(\frac{n}{e}\right)^n \cdot \sqrt{2 \pi n}$

N.b.: : Der Relative Fehler $\frac{\epsilon}{n!}$ ist bei großem $n$ klein. Das gilt nicht notwendigerweise für den absoluten Fehler. Es gilt: $n! = \left(\frac{n}{e}\right)^n \cdot \sqrt{2 \pi n} \cdot \left[1 + \mathcal{O}(1/n)\right]$

Potenzsummen

Endliche Reihen

Hintergrundinformation in den Artikeln Summe und Reihe. Erklärungen zum Summenzeichen ebenfalls im Artikel Summe.

Rechenregeln

$\sum_{i=1}^{n}c = n \cdot c$ (Summation über n konstante Glieder ist soviel wie Multiplikation mit n)

$\sum_{i=m}^{n}c = (n-m+1) \cdot c$ (Summation über n-m+1 konstante Glieder)

$\sum_{i=m}^{n}c \cdot a_i = c \cdot \sum_{i=m}^{n}a_i$ (Konstanter Faktor kann vor das Summenzeichen gezogen werden)

$\sum_{i=m}^{n}(a_i + b_i) = \sum_{i=m}^{n}a_i + \sum_{i=m}^{n}b_i$ (Reihenfolge der Summanden kann beliebig geändert werden)

Arithmetische Reihen

$\sum_{i=1}^n i = \frac{n(n+1)}{2}$ (Summe der ersten n natürlichen Zahlen)

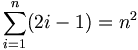
$\sum_{i=1}^n (2i-1) = n^2$

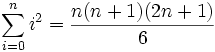
$\sum_{i=0}^n i^2 = \frac{n(n+1)(2n+1)}{6}$

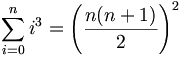
$\sum_{i=0}^n i^3 = \left(\frac{n(n+1)}{2}\right)^2$

Geometrische Reihe

$\sum_{i=0}^n q^i = \frac{q^{n+1}-1}{q-1}$ (geometrische Reihe)

$\sum_{i=0}^{\infty} q^i = \frac{1}{1-q} \qquad \mbox{mit } q<1$ (unendliche geometrische Reihe)

Binomische Reihen

$\sum_{i=0}^{n} {n \choose i} = 2^n$ (siehe Binomialkoeffizient)

$\sum_{i=0}^{n} (-1)^i{n \choose i} = 0 \qquad ( f \ddot ur\ alle\ n>0)$

$\sum_{k=0}^{n}{n \choose k} a^{k}b^{n-k} = (a+b)^n \qquad (a,b \in \mathbb{R} \ und \ n \in \mathbb{N})$ (allgemeine Binomische Formel mit natürlichen Exponenten)

$\sum_{i=0}^{n} {n \choose i} q^i = ( 1 + q)^n$ (siehe Binomischer Lehrsatz)

$\sum_{i=0}^{n-1} {i \choose k} = {n \choose k+1}$

Prozentrechnung

G = Grundwert, p = Prozentsatz, W = Prozentwert

$W = G \cdot {p \over 100} \quad\mbox{oder}\quad p = {W \over G} \cdot 100 \quad\mbox{oder}\quad G = {W \cdot 100 \over p}$

Zinsrechnung

Bezeichnungen

K0 = Anfangskapital

Kn = Endkapital (nach n Zinsperioden)

n = Laufzeit

p = Zinsfuß (Zinssatz in Prozent)

i = Zinssatz (mit i = p/100)

q = Zinsfaktor (mit q = 1 + i)

r = Rentenrate

R0 = Rentenbarwert (zum Zeitpunkt t = 0)

Rn = Rentenendwert (nach n geleisteten Rentenzahlungen)

r = konstante Rentenrate oder Rate

n = Anzahl der Rentenperioden (Anzahl der Jahre, die der Rentenvorgang andauert)

p = Zinssatz der Verzinsung der Rentenraten bzw. des Kapitalbestandes

Als Zinsperiode wird i.d.R. das Kalenderjahr, eingeteilt in 12 Monate mit je 30 Zinstagen gewählt.

Einfache Zinsrechnung:

Endkapital: $\mathbf{K_n = K_0 * (1+ ni)}$

Zinseszins:

Endkapital: $\mathbf{K_n = K_0 * q^n}$

Rentenrechnung

Je nachdem, zu welchem Zeitpunkt innerhalb der zugehörigen Zeitperiode die Rente zur Auszahlung kommt, unterscheidet man zwischen einer vorschüssigen Rente (pränumerando), wenn sie am Anfang, und einer nachschüssigen Rente (postnumerando), wenn sie am Ende des zugehörigen Zeitintervalls ausgezahlt wird.

Rentenrechnung (Nachschüssige Rentenzahlungen)

Rentenrate für R0 : $\mathbf{r(na) = R_0 * q^n * \left(\frac{q - 1}{q^n - 1}\right)}$

Rentenrate für Rn : $\mathbf{r(na) = R_n * \left(\frac{q - 1}{q^n - 1}\right)}$

Rentenendwert: $\mathbf{R_n(na) = r * \left(\frac{q^n - 1}{q - 1}\right)}$

Rentenbarwert: $\mathbf{R_0(na) = \left(\frac{r}{q^n}\right) * \left(\frac{q^n - 1}{q - 1}\right)}$

Rentenrechnung (Vorschüssige Rentenzahlungen)

Rentenrate für R0=:

Rentenrate für Rn:r* q^n -1/q-1

Rentenendwert: =

Rentenbarwert: =

Abschreibung

Jährlicher (j) Abschreibungsbetrag (Lineare Abschreibung)

$r = \frac{K_0 - K_n}{n}$

Jährlicher Abschreibungsbetrag (Geometrisch degressive Abschreibung)

$\mathbf{r_j = K_0 * q^{j-1} * i}$

Zurück

Inhaltsverzeichnis

DIPLOMARBEITEN UND BÜCHER

Diplomarbeiten zum Runterladen:

Architektur / Raumplanung
Betriebswirtschaft - Funktional
Erziehungswissenschaften
Geowissenschaften
Geschichtswissenschaften
Informatik
Kulturwissenschaften

Medien- und Kommunikationswissenschaften
Medizin
Psychologie
Physik
Rechtswissenschaft
Soziale Arbeit
Sozialwissenschaften

	JOBS