Zeichen + Regeln --> Wort
Wort + Regeln --> Satz

Aus einer festgelegten Menge von Zeichen werden nach bestimmten Regeln Worte gebildet, die selbst wieder nach festen Regeln zu Sätzen vereinigt werden. Ein Text besteht dann aus einer Folge von Sätzen. Dieser formale Aufbau einer Sprache heißt Grammatik oder Syntax der Sprache. Die Syntax beschreibt im wesentlichen die Regeln, die Sie beachten müssen, damit die Form des Textes richtig ist.

Die Syntax ist auch bei Worten wie BARTSCHE, DRAUDELN, GRUBBEND oder ZERWANKELMÜTIGKEIT und Sätzen folgender Art völlig in Ordnung: DER COMPUTER BETRITT DEN RASEN. DER HIMMEL WEIGERT SICH, GEMÄß VERORDNUNG 25A DEN DUSCHVORHANG ZU WABELN. ES IST PHANTASTISCH, WIE UNMÖGLICH ES IST, DAß EINE MENGE VON WÖRTERN KEINEN SINN ERGIBT. Aber diese Worte und Sätze, die von der Syntax her richtig (also syntaktisch korrekt) sind, ergeben keinen Sinn, keinen Inhalt, sie bedeuten nichts. Der Sinngehalt eines Satzes oder Wortes muß also ebenfalls festgelegt werden. Das bedeutet, wenn Sie ein Wort schreiben, müssen Sie die Bedeutung des Wortes kennen. Wer MAUS schreibt und dabei an einen großen, grauen Dickhäuter denkt, verstößt gegen jene Regeln der Sprache, die für den Sinngehalt wesentlich sind, die Regeln der Semantik. Mit der Erkenntnis, daß die Syntax einer Sprache ohne eine ausreichende Definition der Semantik nicht für die Normierung der Sprache ausreicht, ist die erste der beiden anfangs gestellten Fragen beantwortet. Es stellt sich jetzt die Frage, was in einer normierten Sprache alles vorhanden sein muß, um Algorithmen zu beschreiben.
Also benötigt eine algorithmische Sprache Möglichkeiten zur Beschreibung der Eingabe- und Ausgabedaten und zur Beschreibung der Verarbeitungstätigkeit. Die Beschreibung der Daten muß die Art der Daten, (z.B.: Zahlen, Striche, Texte, usw.) sowie die Anzahl der Daten enthalten. Die Beschreibung der Tätigkeiten soll der menschlichen Denkweise möglichst gut angepaßt sein, muß aber trotzdem normiert sein. Dazu ein Beispiel:

1. Wenn es regnet, nehme ich den Schirm mit, sonst nicht.
2. Regnet es, so nehme ich den Schirm mit, sonst halt nicht.
3. Ich nehme den Schirm nur dann mit, wenn es regnet.
4. Nur falls es regnet, nehme ich den Schirm mit.
5. Ich nehme, sollte es regnen, den Schirm mit, sonst nicht.
6. Dann und nur dann, wenn es regnet, nehme ich den Schirm mit.

Eine Normierung tut not, denn alle diese Sätze haben dieselbe Bedeutung. Also entwerfen wir die Syntaxregel:

WENN <Bedingung> DANN <Erfüllt-Aktion> SONST <Nicht-erfüllt-Aktion>

Dann lautet das Beispiel:

WENN es regnet DANN ich nehme Schirm mit SONST ich lasse Schirm zu Hause;

Es gibt nur eine Möglichkeit, das ganze noch anders darzustellen, und zwar:

WENN es regnet nicht DANN ich lasse Schirm zu Hause SONST ich nehme Schirm mit;

Aufgrund der Normierung der algorithmischen Sprache bleibt von den vielen Ausdrucksvariationen der natürlichen Sprache nur noch eine einzige Version übrig. Abkürzungen und Umstellungen sind nicht mehr zulässig. Die Sätze müssen immer in der vorgeschriebenen Reihenfolge aufgeschrieben und die Wörter immer ausgeschrieben werden. Wie in der natürlichen Sprache gibt es auch in einer algorithmischen Sprache zahlreiche festgelegte Worte, die sich nicht auf Gegenstände oder Tätigkeiten beziehen, sondern der Verbindung der Worte zu Sätzen dienen. Im Deutschen sind dies zum Beispiel die Präpositeonen oder die Konjunktionen; im letzten Beispiel waren es die Worte WENN, DANN und SONST. Diese Worte dienten der Verbindung der Sätze: es regnet ich nehme Schirm mit ich lasse Schirm zu Hause Die drei "Schlüsselworte" verbinden die genannten Sätze in festgelegter Weise; man nennt sie daher auch Wortsymbole. Die im Beispiel gewählte Syntax:

WENN <Bedingung> DANN <Erfüllt-Aktion> SONST <Nicht-erfüllt-Aktion>

wurde so gewählt, daß auf Grund der Kenntnis der deutschen Sprache der Sinn des "Gebildes" ungefähr klar wird. Bedingung steht für einen Satz, der nach anderen Regeln gebildet werden muß, wie die Sätze hinter den Worten DANN und SONST und der, wie es von einer Bedingung erwartet wird, entweder erfüllt oder nicht erfüllt sein muß. Ist die Bedingung erfüllt, wird die Tätigkeit: <Erfüllt-Aktion> ausgeführt, im anderen Fall wird die mit <Nicht-Erfüllt-Aktion> bezeichnete Aktion ausgeführt. Somit hätten wir die Syntax und die Semantik unseres Beispiels definiert. Natürlich muß auch die Reihenfolge der Bearbeitung festgelegt werden: Prüfe zuerst die Bedingung und führe dann die entsprechende Tätigkeit aus. Die Wortsymbole sind also festgelegte Worte mit fest definierter Bedeutung. Sie werden in den algorithmischen Sprachen meist durch Symbolzeichen wie "+" für die Addition oder "/" für die Division ergänzt. Auch die Bedeutung dieser Zeichen ist festgelegt und nicht zu ändern. Die Menge aller Wort- und Zeichensymbole bildet zusammen mit der Beschreibung von Syntax und Semantik die Definition einer algorithmischen Sprache. Die Symbole dürfen auch in keiner anderen Bedeutung verwendet werden als in der festgelegten. Die Zahl der Symbole sollte so klein wie möglich, aber trotzdem so universell wie möglich sein. Die Vorteile von wenigen, der menschlichen Denkweise angepaßten Symbolen und Zeichen liegt auf der Hand:

• Wenig Symbole erfordern geringen Lernaufwand sowohl für Syntaxregeln als auch für die Semantik.
• Eine geringe Anzahl von Symbolen kann auch durch ein relativ kurzes und effektives Übersetzungsprogramm erkannt und ausgewertet werden.
• Die Universalität der Symbole soll verhindern, daß ein Programmierer "um die Ecke denkt".

Mit den Symbolen alleine kommt die algorithmische Sprache aber immer noch nicht aus, sie möchten ja den Sätzen einen Inhalt geben und den Dingen die Sie behandeln und den Tätigkeiten einen Namen geben. Erinnern Sie sich noch an das Verfahren "S". "S" war dabei ein völlig willkürlich gewählter Name für das Verfahren. Anschließend wurde für das gleiche Verfahren ein anderer, ebenfalls willkürlicher, aber einleuchtenderer Name gewählt: "Verfahren zur Bündelung von Strichen in Fünfergruppen". So wie dort die Namen der Verfahren frei gewählt wurden, können auch die Namen für Dinge, Daten, Personen, Verfahren und Tätigkeiten in einer algorithmischen Sprache frei gewählt werden. Damit Sie sich bei den frei gewählten Bezeichnungen später auch auskennen, sei Ihnen hier erklärt, was mit einer solchen Bezeichnung eigentlich benannt wird:
Der Gegenstand der Benamselung wird zuerst durch seinen Namen und seine Art bekanntgemacht (z. B.: Zahl, Tätigkeit, Person, Menge, Buchstabe, Operation, Unteralgorithmus, usw.). Ferner wird er charakterisiert durch die Tätigkeiten, die auf ihn angewendet werden. Steht zum Beispiel irgendwo "X/12" und jemand fragt: "Was ist X?", können Sie nur antworten: "Es handelt sich um irgendetwas, das durch 12 geteilt wird". So eine Antwort ist aber recht unbefriedigend. Als Lehre sollten Sie daraus ziehen, alle Dinge sinnvoll bezeichnen und zusätzliche Erklärungen und Kommentare für den Leser hinzufügen. Beispiel:

Schlechter Stil:	Y = X/12
Guter Stil:	EIERKARTONZAHL = EIERZAHL/12

Das Beispiel enthält die frei gewählten Bezeichnungen: X, Y, EIERKARTONZAHL, EIERZAHL. Es fehlt nur noch die Einordnung der Zahl 12. Es handelt sich hierbei um eine allgemein übliche und allseits bekannte Bezeichnung. Sie wird daher auch in algorithmischen Sprachen als allgemein üblich betrachtet und Standardbezeichnung genannt. Die Ausdrucksmöglichkeiten einer algorithmischen Sprache werden also durch Wortsymbole, Symbolzeichen, Standardbezeichnungen und frei wählbare Bezeichnungen im Rahmen einer (computerübersetzbaren) Syntax festgelegt. Die Semantik der Symbole und Standardbezeichnungen ist vordefiniert und wird vom "Compiler" schrittweise in eine Maschinensprache übersetzt, während die Semantik der frei wählbaren Bezeichnungen von der durch die Syntax festgelegten Deklarationen (Bekanntmachungen) festgelegt wird.

Ideal ist es, wenn eine solche, syntaktisch festgelegte Form mit ihrer Semantik dem Menschen, der die Verarbeitungsvorschrift verfaßt, leicht verständlich und zugänglich ist. Die erzeugten Verarbeitungsvorschriften müssen lesbar und der menschlichen Denk- und Ausdrucksweise angepaßt sein und trotzdem normiert und computerübersetzbar. Seit Mitte der sechziger Jahre werden Programmiersprachen (= algorithmische Sprachen) entwickelt.

Programmiersprachen

FORTRAN (FORmula TRANSlator) ist eine der ersten und am weitesten verbreiteten Sprachen. Sie ist hauptsächlich für wissenschaftlich-technische Anwendungen bestimmt.

ALGOL (ALGOrithmic Language) ist für die Bearbeitung mathematischer Probleme und für wissenschaftliche Anwendungen besonders geeignet. Die Sprache wurde ständig weiter ausgebaut und verbessert (ALOGOL 60, ALGOL 68).

COBOL (COmmon Business Oriented Language) wurde entwickelt als Standardsprache für kommerzielle Berechnungen. Manche Anweisungen beziehen sich unmittelbar auf Lohnabrechnung oder Rechnungswesen.

BASIC (Beginners All-purpose Symbolic lnstruction Code) ist eine einfache Sprache, die benutzt wird, um in Computer-Programmierung einzuführen. Sie ist einfach zu erlernen, geht aber nicht sehr weit. Ihre Schwächen sind Grund dafür, daß sie kaum noch im Unterricht eingesetzt wird.

LISP (LIST Processing language) wird weithin benutzt in Programmen, mit denen Zeichen von mathematischen Symbolen bis hin zu den Zeichen der Umgangssprache zu verarbeiten sind. Eine Hauptanwendung liegt im Bereich der Untersuchungen zur künstlichen Intelligenz.

Pascal (benannt nach dem Mathematiker und Philosophen Blaise Pascal) wurde für den Einsatz im Informatikunterricht entwickelt. Diese Sprache gehört zur Algol-Familie und eignet sich besonders für wissenschaftliche Probleme. Da Pascal als Lehr-Programmiersprache gedacht war, soll die Entwicklung dieser Sprache etwas genauer dargestellt werden. Niklaus Wirth verfolgte dabei u.a. die folgenden Ziele:

1. Er wollte eine Sprache für den Unterricht schaffen, die einerseits die in allen Sprachen durchgängig vorkommenden Konzepte enthielt und andererseits Inkonsistenzen und unnötige Details vermied.
2. Er wollte eine Standardsprache entwickeln, die preiswert war und sich leicht auf jedem Computer implementieren ließ.

In diesem Sinne ist Pascal so etwas wie eine alIgemeinverständliche Sprache für das Programmieren geworden. Sie läßt sich leicht erlernen und bildet eine gute Grundlage für die Aneignung anderer Sprachen. Man kann sagen: Wer Pascal beherrscht, lernt BASIC an einem Nachmittag. Und für FORTRAN braucht er nicht mehr als ein bis zwei Wochen.
Einer der Vorzüge von Pascal gegenüber den früher entwickelten Sprachen besteht darin, daß man die Programme fast mit den gleichen Formulierungen wie die Lösung des Problems schreiben kann. Die reservierten Wörter, sie bilden das Gerüst von Pascal, sind der englischen Umgangssprache entnommen. Wer Englisch kann, liest ein geschickt gemachtes Pascal-Programm wie eine umgangssprachliche Beschreibung des Weges, der das gestellte Problem löst. Und wenn man ein Problem aufbereitet, gelangt man sehr schnell von der umgangssprachlichen Formulierung zum Pascal-Programm.

C Die Entwicklung der Programmiersprache C ist eng mit der des Betriebssystems UNIX verknüpft. Nachdem die erste UNIX-Version noch in Assembler erstellt worden war (1969), entwickelte Ken Thomson 1970 die Sprache B zur Irnplementierung eines UNIX-Systems für eine PDP-7-Maschine. Aus der mit zu vielen Schwächen behafteten Sprache B entwickelte Dennis Ritchie 1972 C. Seit 1973 ist das Betriebssystem UNIX fast vollständig in C geschrieben. Zunächst gab es keinen offiziellen Sprachstandard. Statt dessen erreichte die Sprachdarstellung in einem Lehrbuch - deutsch: Kemighan, Ritchie; Programmieren in C, Hanser Verlag 1983 - den Status eines Quasi-Standards (Kernighan-Ritchie-Standard). Kleinere Erweiterungen und Verbesserungen führten zum ANSI-Standard. Die Sprache C++ wurde Anfangs der 80er Jahre von Bjarne Stroustrup an den Bell Laboratories entwickelt. Es handelt sich dabei um einen Zusatz für C.
C ist eine Sprache der 3. Generation (strukturierte Sprache) und gehört neben FORTRAN und Pascal zu den wichtigsten Höheren Programmiersprachen im Ingenieurbereich. Die wesentlichen Merkmale der Sprache sind:

• breites Anwendungsspektrum
• knappe Befehle (short is beautiful)
• sehr klares Sprachkonzept.

Was oben als Vorteil erscheint, erweist sich als Nachteil bezüglich der Erlernbarkeit als "Erstsprache". Die "kappen Befehle" könnte man etwas böswillig auch als kryptisch bezeichnen und das "klare Sprachkonzept" verlangt vom Programmierer Grundkenntnisse über Aufbau und Arbeitsweise von Computern, deutlich mehr als Pascal und FORTRAN. Allerdings steigen diese Grundkenntnisse bei der jungen Generation von Jahrgang zu Jahrgang. Fast jeder (interessierte) kann mit einem PC umgehen. Viele haben bereits gelernt, kleinere Probleme in Basic oder Pascal zu lösen. Und so kann man es heute wagen, ernsthaft mit C zu starten. Die Mühe lohnt sich!

Mittlerweile gibt es neben den vorgenannten aufschreibungsorientierten Programmiersprachen auch graphische Programmiersprachen. Populäre Firmenübergreifende Standards sind mir unbekannt. Idee ist es mittles graphischer Verknüpfung von Piktogrammen, die stellvertretend jeweils unterschiedliche Grundfunktionen darstellen, ein Programm änlich einer Zeichnung zu entwerfen. LabView ist ein solches Produkt mit einer solchen Programmierumgebung. LabView wird in der Meßtechnik häufig eingesetzt. Virtuelle Meßgeräte (Softwarefunktionen), wie Voltmeter, Ampermeter, Spektrumsanalysator etc werden als Piktogramme dargestellt und der Meßaufbau, die Verkabelung, durch graphische Linien, die die Geräte an den unterschiedlichen Buchsen verbinden. Meßvorgänge werden per Knopfdruck in der Graphik ausgelöst, und die Ergebnisse graphisch dargestellt. Vorteil dieser Art der Programmierung ist, daß sich der Anwender voll auf seine 'Welt' konzentrieren kann, ohne eine Programmiersprache lernen zu müssen. Ob sich diese Art der Programmierung auch in anderen Bereichen durchsetzt bleibt abzuwarten.

Algorithmen und das Lösen von Aufgaben

Beispiel: Vertauschen von Zahlen

Nimm den Zähler und den Nenner auf.
Gib dem Zähler den Wert des Nenners.
Gib dem Nenner den Wert des Zählers.

Bemerken Sie den Fehler, der auftreten würde, wenn der Computer diese Anweisungsfolge pedantisch ausführt (und das tut er tatsächlich!)? Beide Variablen, die für den Zähler und die für den Nenner, hätten zum Schluß den gleichen Wert, den des ursprünglichen Nenners. Das liegt daran, daß man den Wert des ursprünglichen Zählers nicht zwischengespeichert hat. Ein Algorithmus für den Computer muß das ausdrücklich vorsehen:

Nimm den Zähler und den Nenner auf.
Speichere den Zähler.
Gib dem Zähler den Wert des Nenners.
Gib dem Nenner den gespeicherten Wert.

Beispiel: Fallentscheidung

Lösung 1:
Prüfe, ob X den Wert 2 besitzt.
Falls ja, setze X auf 1.
Setze X auf 2.

Lösung 2:
Prüfe, ob X den Wert 2 besitzt.
Falls ja, setze X auf 1.
Sonst setze X auf 2.

Lösung 3:
Setze X auf das Ergebnis der Rechnung 3 - X.

Welche Lösung ist richtig? Erstaunlicherweise keine! Bei der ersten Lösung hat X nach Ablauf immer den Wert 2. Die beiden anderen Lösungen scheinen beide richtig, wobei die dritte zwar elegant erscheint, aber für den Leser des Algorithmus schwerer verständlich ist. Sie sind aber deshalb falsch, weil nicht überprüft wird, ob X einen der beiden zulässigen Werte (1,2) besitzt. Richtig wäre also:

Lösung 2:
Prüfe, ob X den Wert 1 oder den Wert 2 besitzt.
Falls nein, melde den Fehler und beende die Arbeit.
Prüfe, ob X den Wert 2 besitzt.
Falls ja, setze X auf 1.
Sonst setze X auf 2.

Diese Beispiele sollen Sie nicht in Panik versetzen. Sie brauchen nicht an Ihren Fähigkeiten, Algorithmen für den Computer zu entwerfen, zu verzweifeln. Diese Fähigkeiten sind keineswegs unveränderlich, sie lassen sich sehr wohl entwickeln und trainieren.

Denken und Arbeitsweisen schulen

Es darf die systematische Arbeitsweise (Arbeitsdiziplin) nicht vergessen werden: Lernen und Verbessern erfordert einen Rückkopplungsprozeß. Allgemein: Dazu definiert sich der Ingenieur ein quantitativ erfaßbares Ziel und versucht es zu erreichen. Dabei ist es wichtig ein objektives Maß (Metrik) dafür zu haben wie nahe er dem Ziel ist. Aus der Abweichung ergibt sich Steuerungsbedarf im Bestreben dem Ziel näher zu kommen. Dieser interative Prozeß der Zielanäherung kann nur verbessert (Optimierung) und an Andere weitergegeben (Erfahrungsaustausch) werden, wenn er dokumentiert und objektiv nachvollziehbar (entspricht in der Mathematik: 'nachrechenbar' ) ist. Für die Softwareentwicklung bedeutet dies: Alle Arbeitsschritte, Metriken und Denkprozesse müssen nachvollziehbar (schriftlich) dokumentiert sein, inklusive der getroffenen technischen Entscheidungen. Nur so kann man selbst und alle zusammen an Können gewinnen.

Kundenanforderungen, Softwareentwurf, Programmierstil und Softwarequalität

Die Problemlösung läft also meist nach folgendem Schema ab:

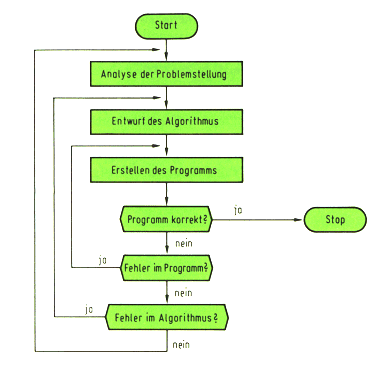
Das wichtigste ist beinahe vergessen worden: Die Kundenanforderungen! Es ist erstaunlich wie viel Software am eigentlichen Nutzer vorbei entwickelt wird, nur weil der Entwickler denkt er weiß, was der Kunde braucht, und sich nicht erkundigt, was der Kunde wirklich will. Oftmals verliert während des Entwurfs der Entwickler den Kunden aus den Augen und er baut technikverliebt nicht gewollte Komplexität ins Programm ein, die meistens viel Zeit beim Testen kostet. Eine erste Faustformel könnte lauten:

Zurück

Inhaltsverzeichnis

Nächste

Diplomarbeiten zum Runterladen: