Jedes Problem, dessen Lösung durch einen Algorithmus beschrieben werden kann, ist im Prinzip durch einen Computer lösbar.

Aus dieser Aussage können Sie zwei Schlüsse ziehen:

1. Ein Computer ist ein Werkzeug, welches Ihnen bei der Lösung gewisser Probleme hilft.
2. Ein Algorithmus ist eine Art Anleitung oder Vorschrift, wie man zu einem Problem eine Lösung findet.

Ein Algorithmus ist eine eindeutige Beschreibung eines endlichen Verfahrens zur Lösung einer bestimmten Klasse von Problemen.

Zu viel auf einmal? Wir werden im nächsten Abschnitt auf die einzelnen Eigenschaften eines Algorithmus noch genauer eingehen. Zunächst wollen wir den Begriff des Algorithmus jedoch mit "Leben" füllen, damit Sie ganz konkrete Vorstellungen damit verbinden können.

Alltagsalgorithmen

Jeder von uns kann in einer Telefonzelle erfolgreich telefonieren. Nehmen wir an, wir hätten einen Gast von einem fernen Planeten, der perfekt deutsch spricht und liest, der aber noch niemals eine Telefonzelle benutzt hat (vermutlich, weil seinesgleichen per Telepathie kommuniziert). Er soll nun von uns auf einem Blatt Papier eine exakte Handlungsanweisung für die Benutzung dieser Telefonzelle erhalten, damit er uns nach dem Shopping anrufen kann. Es wird sich also um ein Ortsgespräch handeln, und wir unterstellen, daß unser Gast einige Groschen in der Tasche hat und unsere Telefonnummer kennt. Außerdem setzen wir einige Randbedingungen als bekannt voraus, obwohl gerade diese in der Praxis oft zu großen Realisierungsproblemen führen, hier z. B. die Frage: "Was ist der Hörer und wie dann wir herum wird er gehalten?".

Von Personen, die sich bisher mit der algorithmischen Lösung solcher Alltagsprobleme nicht beschäftigt haben, wird meist folgende Handlungsanweisung genannt:

1. Nimm Hörer ab;
2. Wirf 20 Cent ein;
3. Wähle ...

Tatsächlich lautet die korrekte Handlungsanweisung, nach der wir alle in der Praxis vorgehen:

1. Nimm Hörer ab;
2. Falls Dauerton vorhanden, dann wirf zwei Cent ein, sonst hänge Hörer ein und verlasse Telefonzelle;
3. Falls eine Münze durchfällt, dann prüfe, ob diese Münze schon einmal durchgefallen ist. Falls ja, tausche sie aus, sonst werfe sie erneut ein;
4. Wähle ...

1. Nimm Hörer ab;
2. Falls Dauerton vorhanden,
   dann wirf zwei Cent ein,
   sonst hänge Hörer ein und verlasse Telefonzelle;
3. Falls ein Cent durchfällt,
   falls die Münze schon einmal durchgefallen ist,
   dann wechsle sie aus,
   sonst werfe sie erneut ein,
   sonst wähle;
4. ...

Soll der Algorithmus jedoch von einer Maschine (einem Computer) ausgeführt werden, dann müssen diese Anweisungen viel präziser formuliert und alle möglichen Sonderfälle berücksichtigt werden. Auch wenn man selbst nicht programmiert, so ist diese Art zu denken eine wichtige Grundlage für eine sinnvolle Anwendung von Computern.

Eine weitere Gemeinsamkeit der aufgeführten Alltagsalgorithmen besteht darin, daß sie Anweisungen zur Manipulation von Objekten geben. Der Algorithmus oben beschreibt beispielsweise, wie die Objekte Hörer, Münze, Tastenfeld usw. zu manipulieren sind. Besonders deutlich tritt diese Eigenschaft bei Kochrezepten zum Vorschein. Als Beispiel betrachten wir die Zubereitung einer Gulaschsuppe.

Algorithmus "Gulaschsuppe zubereiten"

Hilfsobjekte:
Herd, Kochgeschirr

Anweisungen:

1. Fleisch und Zwiebeln würfeln
2. in Schmalz andünsten
3. mit Mehl bestäuben und kurz anrösten
4. Tomatenmark zugeben
5. mit Wasser auffüllen
6. garen
7. mit Salz, Paprika und Majoran abschmecken.

• einem Deklarationsteil, in dem die zu manipulierenden Objekte deklariert werden
• einem Aktionsteil, in dem die auszuführenden Aktionen in Form von Anweisungen beschrieben werden.

Eigenschaften von Algorithmen

• Eindeutige Beschreibung
  Bei der Verwendung einer natürlichen Sprache wie Deutsch, Englisch, Französisch usw. läßt es sich nicht vermeiden, daß gewisse Wörter und Sätze eine Mehrdeutigkeit beinhalten, d. h. daß man sie verschieden interpretieren kann. Denken Sie z. B. an folgende Wörter:
  • Stollen: Weihnachtsgebäck oder Gang im Bergwerk oder Teil eines Fußballschuhes.
  • Bund: Zusammenschluß oder Teil einer Hose.
  • Mutter: Weibliche Person mit Kind oder Teil einer Schraube.
  In einem Algorithmus dürfen solche mehrdeutigen Formulierungen nicht vorkommen. Der "Ausführende" - ganz gleich ob Mensch oder Maschine - darf nie im Zweifel darüber sein, wie eine bestimmte Anweisung zu interpretieren ist.
• Endliches Verfahren
  Ein Algorithmus muß ein endliches Verfahren beschreiben (das Gegenteil wäre ein unendliches). Man meint damit, daß das durch den Algorithmus beschriebene Verfahren nach einer endlichen Zahl von Schritten eine Lösung produziert. Die genaue Anzahl hängt natürlich davon ab, wer den Algorithmus ausführt. Man sagt auch: "Das Verfahren muß terminieren", also zu einem Abschluß kommen. Mit der Endlichkeit hängt ein weiterer Begriff zusammen: die Effizienz. Man sucht zur Lösung eines Problems einen möglichst effizienten Algorithmus (eigentlich müßte man genauer sagen: einen Algorithmus, der ein möglichst effizientes Verfahren beschreibt). Auf Computer bezogen bedeutet das zweierlei:
  1. Die Ausführungszeit soll möglichst kurz sein.
  2. Der Speicherplatzbedarf soll möglichst gering sein.
• Bestimmte Problemklasse
  Ein Algorithmus soll ein Lösungsverfahren für eine ganze Klasse von Problemen beschreiben und nicht nur für ein isoliertes Einzelproblem. Man sagt auch: "Das Verfahren soll allgemeingültig sein." Wir wollen uns diese Eigenschaft an einem ganz einfachen Beispiel klar machen. Nehmen wir einmal an, Sie sollen die Zahlen 7,12 und 16 addieren. Sie könnten das Lösungsverfahren folgendermaßen beschreiben:
  1. Addiere 7 und 12, nenne das Ergebnis SUMME1.
  2. Addiere 16 zu SUMME1, nenne das Ergebnis SUMME2.
  3. Schreibe als Lösung SUMME2 auf.
  Diese Lösungsvorschrift ist nach unserer Definition kein Algorithmus, da sie lediglich für ein ganz spezielles Teilproblem die Lösung liefert. Soll man beispielsweise die Zahlen 7, 12 und 17 addieren, dann kann man diesen Algorithmus nicht mehr verwenden. Ein erster Schritt zur Verallgemeinerung besteht darin, statt der Konstanten 7, 12 und 16 drei Variablen einzuführen, z. B. ZAHL1, ZAHL2 und ZAHL3. Das dadurch beschriebene Verfahren gilt dann für die Addition dreier beliebiger Zahlen. Das Problem, die Summe aus drei Zahlen zu berechnen, gehört aber zu einer allgemeineren Problemklasse, nämlich die Summe aus N Zahlen zu berechnen. Dabei ist N eine natürliche Zahl größer als 1. Unser spezielles Problem, die Zahlen 7, 12 und 16 zu addieren, ist also nur ein Spezialfall dieses allgemeinen Problems für N = 3. Die Lösungsvorschrift für dieses Problem ist dann ein Algorithmus im Sinn unserer Definition. Durch die Forderung nach Allgemeinheit erreicht man also, daß man wenige mächtige Algorithmen erhält und sich nicht in einer Vielzahl von Lösungsvorschriften für Sonderfälle verzettelt.

  Weitere Punkte, die auch oft als Eigenschaften von Algorithmen gefordert werden, sich aber aus den obigen Eigenschaften ergeben, sind:

  1. Vollständigkeit der Beschreibung
     Es muß eine komplette Anweisungsfolge vorliegen. Eine Bezugnahme auf unbekannte Information darf nicht enthalten sein.
  2. Wiederholbarkeit des Algorithmus
     Im Sinne eines physikalischen Experiments muß man die Ausführungen eines Algorithmus beliebig oft wiederholen können und jede Wiederholung muß bei gleichen Eingabedaten das gleiche Resultat liefern (Reproduzierbarkeit).
     Ist ein Algorithmus endlich und definit so ergibt sich diese Forderung automatisch.
  3. Korrektheit des Algorithmus
     Diese Forderung ist zwar selbstverständlich, aber in der Praxis ist die Korrektheit nur sehr schwer nachzuweisen. Man bedient sich daher Tests, bei denen für die vorgegebenen Eingabedaten das Ergebnis bereits bekannt ist, und vergleicht dann die erzeugten Ausgabedaten mit den Ergebnissen. (Ein solcher Test ist insofern problematisch, da alle möglichen Fälle abgedeckt werden müssen. Im Extremfall muß dieser Test sogar für jede mögliche Eingabe durchgeführt werden.) Der Begriff der Korrektheit nimmt zwar in der Literatur einen sehr großen Raum ein, da es nicht trivial ist, die Korrektheit nachzuweisen, er ist jedoch für die Definition eines Algorithmusbegriffes nicht erforderlich.

  Neben diesen Eigenschaften gibt es noch weitere Eigenschaften von Algorithmen, die sich auf die Art und Weise der Ausführung des Algorithmus beziehen. Hier sind zu nennen:

  • Die Effizienz der Beschreibung und der Ausführung (umständlich oder einfach).
  • Die Art der Ausführung einzelner Anweisungen (sequentiell oder parallel).
  • Die Komplexität bei der Ausführung. (Sie ist ein Maß für den Aufwand bei der Durchführung eines Algorithmus).

  Zusammenfassen lassen sich alle diese Eigenschaften in einer kurzen aber präzisen Definition des Begriffs Algorithmus.

  Algorithmus Eine Bearbeitungsvorschrift heißt Algorithmus, wenn sie folgende Eigenschaften erfüllt: Die Vorschrift ist mit endlichen Mitteln beschreibbar. Sie liefert auf eine eindeutig festgelegte Weise zu einer vorgegebenen Eingabe in endlich vielen Schritten genau eine Ausgabe.

  Da man nicht alle Bearbeitungsvorschriften durch eindeutige Folgen von Anweisungen als Algorithmus darstellen kann, wurde im Laufe der Zeit der Begriff ausgedehnt. Man unterscheidet heute zwischen deterministischen und nicht-deterministischen Algorithmen. Enthält ein Algorithmus elementare Anweisungen, deren Ergebnis durch einen Zufallsmechanismus beeinflußt wird, so heißt dieser Algorithmus nicht-deterministisch. Liefert er bei der gleichen Eingabe immer die gleiche Ausgabe, so heißt er deterministisch.

  Spielen wir nun noch ein Beispiel für eine Verfahrensbeschreibung durch. Beschreibung des Verfahrens "S":

  (S1) Wenn keine Striche mehr in der Eingabe vorhanden sind, so höre auf.
  (S2) Nimm einen Strich aus der Eingabe weg. Wenn bereits vier Striche ungebündelt in der Ausgabe liegen, lege einen Querstrich über sie; andernfalls füge einen Strich in der Ausgabe hinzu. Dann gehe nach (S1).

  Bei dieser Art der Darstellung eines Verfahrens gilt die Regel: Wenn man alle Handlungen eines Schritts durchgeführt hat und nicht ausdrücklich durch "höre auf" oder "gehe nach" etwas anderes gesagt bekommt, so geht man zum nächsten Schritt.

  Sie haben zwar jetzt die Beschreibung eines Verfahrens erhalten, seinen Nutzen erkennen Sie aber erst, wenn Sie wissen, was in der EINGABE vorhanden ist und wie die AUSGABE aussieht. Denken Sie nochmal an den Informationsfluß. Das Kennzeichen der Datenverarbeitung wird Ihnen immer wieder begegnen: EINGABE - VERARBEITUNG - AUSGABE. Die Eingabe des Verfahrens "S" besteht aus einer Anzahl von Strichen, die irgendwie angeordnet sind, z. B. wie hier:

  

  Führen Sie jetzt das Verfahren "S" durch. In (S2) ist eine Bedingung; wir müssen diese prüfen und, wenn sie erfüllt ist, die dahinterstehende Anweisung ausführen. Als Ausgabe erhält man was hier dargestellt ist.

  

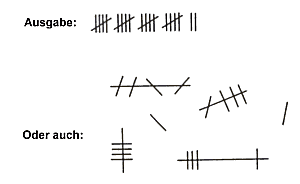
  Gewünscht war natürlich das linke Beispiel. Also hat unsere Verfahrensbeschreibung noch etliche Schwachstellen. Sie müßte präzisiert werden, etwa durch: "Füge einen Strich von 8 mm Höhe parallel zu den anderen Strichen und parallel zur langen Kante des Papiers im Abstand von 0,5 mm von dem vorhergehenden auf derselben Grundlinie wie die anderen an. Man könnte der Beschreibung auch noch einen vernünftigen Namen geben: "Verfahren zur Bündelung von Strichen in Fünfergruppen".

  Damit ein Verfahren einem Computer mittels einer Programmiersprache erklärt werden kann, muß es den folgenden Bedingungen genügen:

  

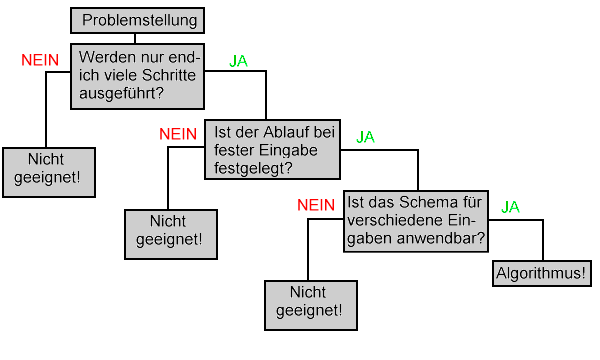
  Der Begriff Algorithmus ist ein zentraler Begriff der Informatik. Er baut immer auf einer Menge von Grundoperationen auf.

  Was ist Programmieren?

  Das Verfahren "S" ist in deutscher Sprache geschrieben, die für ein und dieselbe Handlung oft mehrere Ausdrücke erlaubt. So läßt sich "wegnehmen" auch durch "entfernen" oder "streichen" ersetzen. Auch die Sätze lassen sich auf verschiedene Art konstruieren: "Wenn keine Striche mehr in der Eingabe sind, höre auf", "sind keine Striche mehr in der Eingabe, dann Ende", "Schluß, falls keine Striche mehr in der Eingabe sind", "Solange noch Striche vorhanden sind gehe zu S2, sonst höre auf." .
  Da dem Computer alles genau erklärt werden muß, was er tun soll, müßte ihm erklärt werden, daß die obigen Konstruktionen und Worte die gleiche Bedeutung besitzen. Man muß dann aber auch klären, wann die Begriffe nicht das Gleiche bedeuten.

  Die Schwierigkeiten, die dabei entstehen, sind der Grund, weshalb man dem Computer nur eine ganz bestimmte Sorte von Sprachen, sogenannte normierte Sprachen, anbieten darf. Die Programmiersprachen sind normierte Sprachen, die der Beschreibung von Verarbeitungsvorschriften, Datenstrukturen sowie Ein- und Ausgabe dienen.

  Programmieren bedeutet also, einen Computer dazu zu bringen, Algorithmen auszuführen. Dafür müssen wir den Algorithmus so formulieren, daß der Computer ihn versteht - in einer Programmiersprache. Mit dem, was wir bisher wissen, können wir definieren, was man unter einem Programm versteht:

  Ein Programm ist die Formulierung eines Algorithmus in einer Programmiersprache.

  Programme sind also Algorithmen, die in einer besonderen Sprache formuliert sind. Den Begriff "Programmieren" können wir somit wie folgt definieren:

  Unter "Programmieren- versteht man das Aufschreiben eines Algorithmus in einer Programmiersprache.

  Wenn Sie eine höhere Programmiersprache beherrschen wollen, müssen Sie zuerst einmal ihr Vokabular und ihre Grammtik lernen. Zum Verständnis der Programmiersprache müssen Sie zusätzlich auch deren Konzepte erlernen, um die Sie sich bei natürlichen Sprachen nicht kümmern müssen. Bei imperativen Programmiersprachen wie Java sind dies z.B. Variablen, Anweisungen, Prozeduren. Alleine durch das Auswendiglernen von Vokabeln und Grammatikregeln schaffen Sie es jedoch nicht, mit der Programmiersprache umgehen zu können. Sie müssen die Sprache auch konsequent einsetzen und durch ständiges üben Erfahrungen sammeln. Deshalb ist die Bearbeitung der übungsaufgaben in diesem Kurs verpflichtend.

  Das Erlernen einer Programmiersprache ist nicht schwierig, da das Vokabular und die Grammatik nicht besonders umfangreich sind. Was sehr viel schwieriger ist, ist das Programmieren lernen, d.h. das Erlernen des Programmentwicklungsprozesses:

  • Wie komme ich von einem gegebenen Problem hin zu einem Programm, das das Problem korrekt und vollständig löst.
  • Wie finde ich eine Lösungsidee bzw. einen Algorithmus, der das Problem löst.
  • Wie setze ich den Algorithmus in ein Programm um?
  Während das Erlernen einer Programmiersprache ein eher mechanischer Prozess ist, bei dem die Verwendung des Compilers und das Hilfesystem helfen können, ist die Programmentwicklung ein kreativer Prozess, der Intelligenz voraussetzt. An dieser Stelle sind Sie gefragt! Programmieren lernen bedeutet in noch stärkerem Maße als das Erlernen einer Programmiersprache: üben und Erfahrungen sammeln.
  • Schauen Sie sich die Programme anderer Programmierer an und überlegen Sie: Wieso hat der das Problem so gelöst?
  • Denken Sie sich selbst Probleme aus und versuchen Sie, hierfür Programme zu entwickeln.
  • Fangen Sie mit einfachen Aufgaben an und steigern Sie nach und nach den Schwierigkeitsgrad.
  • Ganz wichtig ist: Versuchen Sie Programmierpartner zu gewinnen, mit denen Sie Probleme und Lösungsansätze diskutieren können.

  Der Ausdruck "Programmieren" bezeichnet also im engen Sinn lediglich das Erstellen eines Programms. Oft bezeichnet man jedoch mit "Programmieren" alle Tätigkeiten eines Programmierers, die von der Problemstellung zur fertigen Lösung führen. Das Problemlösen mit Hilfe eines Computers umfaßt folgende Stufen:

  1. Analyse der Problemstellung
  2. Entwurf des Algorithmus
  3. Erstellen des Programms
  4. Prüfen auf Korrektheit
  5. Dokumentation des Programms
  6. Anwendung des Programms

  Ein Programm ist also eine eindeutige, logische Folge von (genormten) bekannten Bearbeitungsschritten endlicher Länge. Beim Computer richten sich diese Befehle an das Steuerwerk. Die Zahl der verschiedenen Befehle ist bei den Computern aus verständlichen Gründen beschränkt. Als Beispiel soll ein Algorithmus aus der Mathematik betrachtet werden: Die näherungsweise Berechnung des Kreisumfangs.

  Algorithmus "Kreisumfang":
  (K1) Nimm den Radius aus der Eingabe.
  (K2) Multipliziere den Radius mit 2,0 und nenne das Ergebnis 'Durchmesser'.
  (K3) Multipliziere den Durchmesser mit 3,1415926 und bringe das Ergebnis in die Ausgabe.

  Dieser Algorithmus liefert beispielsweise zur Eingabe 7,0 die Ausgabe 43,982296. Wenn der Computer das Multiplizieren nicht beherrscht, dann müßte man ihm noch einen Algorithmus, ein Verfahren, für deren Durchführung geben.

  Algorithmus "Multiplikation":
  (M1) Schreibe die beiden Zahlen aus der Eingabe nebeneinander.
  (M2) Nimm die erste Ziffer der zweiten Zahl.
  (M3) Schreibe die erste Zahl sooft untereinander, wie die Ziffer der zweiten Zahl angibt, und zwar so, daß die letzte Ziffer unter der betrachteten Ziffer der zweiten Zahl steht. Für den Fall, daß besagte Ziffer 0 ist, schreibe 0.
  (M4) Falls noch Ziffern in der zweiten Zahl vorhanden sind, nimm die nächste Ziffer und gehe nach (M3).
  (M5) Addiere alle mit (M3) erzeugten Zahlen.
  (M6) Zähle bei dem Ergebnis soviele Stellen von rechts ab, wie beide Eingabewerte zusammen an Stellen hinter dem Komma besitzen. Setze hier das Komma im Ergebnis.
  (M7) Bringe dies Endergebnis in die Ausgabe.

  Beispiel für die Eingaben 3,14 und 14,0:

                                            3,14 x 14,0
                                            -----------
                                                314 
                                                 314 
                                                 314 
                                                 314 
                                                 314
                                                    0
                                            ----------
                                               43,960 
                                         

  Die Ausgabe ist 43,960. Dieser Algorithmus für die Multiplikation kann dann überall dort verwendet werden, wo "multipliziere" steht. Aus dieser Tatsache lassen sich zwei Erkenntnisse gewinnen:

  • Wenn eine komplizierte Tätigkeit öfters benötigt wird, kann man für diese Tätigkeit einen eigenen Algorithmus definieren. Dieser wird dann Unteralgorithmus genannt.
  • Man kann eine Programmiersprache auf eine bestimmte, begrenzte Menge von Operationen und Denkstrukturen beschränken.

  Versuchen Sie doch einmal, den Algorithmus "Kreisumfang" so umzuformen, daß er überall dort, wo multipliziert wird, der Algorithmus "Multiplikation" als "Unteralgorithmus" aufgerufen wird. Auf dieser Idee beruht die Theorie der Softwareentwicklung. Komplizierte und komplexe Strukturen und Tätigkeiten werden durch bekannte Strukturen und einfachere Unteralgorithmen realisiert. Sie werden auch sehen, daß auch Programme auf entsprechend konstruierte "Unterprogramme" zurückgreifen können. Und es sei hier schon angemerkt, daß diese Möglichkeit die wichtigste und mächtigste Eigenschaft der Programmiersprachen ist. Die oben erwähnten komplizierten Strukturen sind genau jene, die der menschlichen Denkweise entsprechen. Zum Beispiel die Struktur:

  "Wenn die Bedingung erfüllt ist, dann tue dies; sonst tue jenes."

  Daß dabei eine ganze Reihe von Handlungen nacheinander erforderlich ist, wird dem Menschen gar nicht bewußt. Zuerst muß die Bedingung ausgewertet werden. Dazu müssen alle Informationen beschafft werden, die zu dieser Auswertung nötig sind. Danach müssen sie verarbeitet werden, bis festgestellt ist, ob die Bedingung erfüllt ist. Erst jetzt können die entsprechenden Tätigkeiten ausgeführt werden, was unter Umständen wieder recht kompliziert werden kann.
  Die höheren Programmiersprachen bieten also schon als Grundoperationen recht komplizierte Dinge an. Ebenso werden komplizierte Denkstrukturen angeboten, die, wie gesagt, dem menschlichen Denken sehr verwandt sind.
  Sie sind normierte Sprachen, die der Beschreibung von Algorithmen dienen. Genaueres über solche "algorithmische Sprachen" sollen Sie im folgenden Abschnitt erfahren. Durch die Anpassung an die menschliche Denkweise wird bei den Programmiersprachen das Schreiben von Algorithmen erleichtert; andererseits läßt sich aus einem Programm eine Beschreibung in natürlicher Sprache zurückgewinnen.

  Die fest vorgeschriebenen Teile der Programmiersprachen orientieren sich meist am Englischen. So wird aus der Struktur

  "Wenn ... dann ... sonst ..."

  in der Programmiersprache C zu

  "if (..) { ... } else { ... }

  Allerdings wurden bei der Konstruktion der höheren Programmiersprachen die Ausdrucksmöglichkeiten so ausgewählt, daß Doppeldeutigkeiten unmöglich sind. Dazu wird die Form der Ausdrucksmöglichkeiten vorgeschrieben und ihre Bedeutung eindeutig und genau erklärt.
  Der entscheidende Punkt bei den höheren Programmiersprachen ist aber folgender. Dadurch, daß die Form der Programme, die in höheren Programmiersprachen geschrieben sind, bestimmten, festen Regeln genügt, können diese Regeln automatisch, also auch von einem Computer (mit einem entsprechenden Programm) analysiert werden. Da zu jeder erkannten Form die zugehörige Bedeutung genau festgelegt ist, kann das Programm automatisch (d. h. wieder von Computer) auf eine andere Form mit der gleichen Bedeutung, jedoch mit einfacheren Grundoperationen und Grundstrukturen umgewandelt werden.
  Die Umwandlung kann so erfolgen, daß sich die Form völlig, die Bedeutung aber überhaupt nicht ändert. Wenn nun diese neue Form in einer, von dem Computer ausführbaren Sprache (Maschinensprache) besteht, so wurde eine höhere Programmiersprache (die der Mensch versteht) in die Maschinensprache (die der Rechner versteht) übersetzt.

  Befehlssatz

  Die einfachste Programmiersprache besteht aus einem Satz von Befehlen. Dies sind die eingebauten Kommandos, sie sind in ihrer Wirkung vergleichbar mit dem, was Sie mit den Tasten Ihres Taschenrechners auslösen. Mit diesen Befehlen lassen sich u.a. arithmetische Operationen ausführen und Werte für die Dauer der Rechnung speichern. Auch gibt es Befehle, mit denen man Werte vergleicht und damit entscheidet, was als Nächstes gemacht wird. Ein Teil der Befehle wird benötigt, wenn man Daten im Speicher ablegen oder von dort zurückholen will. Besondere Befehle befassen sich damit, in einem Programm Sprünge auszuführen, d.h. Programmteile, die im Moment nicht ausgeführt werden sollen, zu überspringen, oder auch um an eine bereits ausgeführte Stelle im Programm zurückzuspringen und sie so zu wiederholen.

  Maschinensprache

  Wenn man die Befehle durchnumeriert, erhält man eine Maschinensprache; das ist der einfachste Programmiercode. in diesem Code kann die Nummer eines Befehls als sein Name verwendet werden. Ein Maschinensprachenprogramm ist nichts weiter als eine lange Folge von solchen Codewörtern.
  In einer Maschinensprache zu programmieren, ist nicht schwer, aber unglaublich mühsam. Zum Glück hatte einer der frühen Programmierer eine brillante Idee, wie man sich die Arbeit erleichtern kann. Wenn man ein Maschinenprogramm schreibt, das kurze Buchstabenfolgen erkennen und in zugehörige Maschinenbefehle übersetzen kann, dann braucht der Programmierer nicht die Codierung der Befehle in der Maschinensprache zu lernen. Stattdessen kann er jeden Maschinenbefehl als "Klartext-Kürzel" (engl. mnemonic) hinschreiben. Die entsprechenden Übersetzungsprogramme, man nennt sie Assembler, wurden bald für alle Computer entwickelt.
  Das Programmieren in einer Assemblersprache ist etwas weniger mühsam. Ein Programm ist eine Folge von Kommandos, die jeweils aus zwei bis vier Buchstaben bestehen und denen Adressen von Speicherplätzen angefügt werden. Zum Beispiel bedeutet das Kommando

  ADD R2, R6

  Addiere den Inhalt des Speicherplatzes R2 zum Inhalt von R6 und speichere die Summe in R6. In welche Befehle dieses Kommando übersetzt wird, können Sie sich verdeutlichen, wenn Sie die Operation an einem Taschenrechner (der einen Speicher hat) mit einer Tastenfolge ausführen.

  Noch bis zum Ende der fünfziger Jahre bestand das Programmieren tatsächlich aus der minutiösen Übersetzung von Befehlen in binär, oktal oder sexadezimal dargestellte Zahlen und deren Aneinanderreihung zu einem sinnvollen Programm. Man bezeichnet diese Tätigkeit mit Codieren. Die Unzulänglichkeiten dieses Verfahrens traten aber mit dem Schneller- und Größerwerden der Computer mehr und mehr hervor:

  • Der Codierer war gezwungen, sein Programm auf die Eigenheiten des spezifischen Computermodells auszurichten. Er benötigte dazu genaueste Kenntnisse aller Details dieser Maschine und deren Befehlssatz. Der Austausch von Programmen zwischen verschiedenen Maschinen wurde dadurch unmöglich, und Kenntnisse der Codiermethoden eines Computers waren oft wertlos für die Codierung eines anderen. Jeder erstellte eigene Programme und war gezwungen, bei der Neuanschaffung eines Computers diese aufzugeben und die Codierarbeit von vorne zu beginnen. Es wurde klar, daß das gezielte Ausrichten von Algorithmen auf die merkwürdigsten Eigenheiten eines bestimmten Computers eine schlechte Verwendung des menschlichen Intellektes war.
  • Der Programmierer wurde durch seine enge Bindung an eine Rechenanlage und die extrem begrenzten Hardwaremöglichkeiten - langsam, wenig Arbeitsspeicher, extrem teuer (mehrere MegaDMs/Rechner)- nicht nur befähigt, sondern sogar ermuntert, alle möglichen Tricks zu erfinden, um aus den Eigenheiten des Computers ein Maximum herauszuwirtschaften. Zu dieser Zeit galten die Programmierer noch als Beigabe des Hardwareherstellers, denn im Vergleich zu den Hardwarekosten, kosteten die Arbeitskräfte kaum was. Als die verzwickte Programmierung in Mode war, verwendeten Programmierer nicht nur viel Zeit zur Erstellung "optimaler" Programme, auch deren Tests stellte sich als äußerst schwierig dar. Es war für einen Mitarbeiter beinahe unmöglich, die Funktionsweise eines fremden Programms herauszubekommen (und oft war es sogar schwierig das eigene zu überblicken). Heute ist das Teuerste die Erstellung von Anwendersoftware. Deshalb vermeiden heutige Programmierer die Anwendung von Tricks um jeden Preis.
  • Der sogenannte Maschinencode enthielt sehr wenig Redundanz, auf Grund deren ein Fehler hätte entdeckt werden können. Bereits kleine Schreibfehler verändern einen Maschinencode in einen anderen gültigen Maschinencode, der aber völlig andere Bedeutung und somit Auswirkungen auf die Funktion des Programms hat. Solche Fehler sind nur sehr schwer zu entdecken, obwohl sie bei der Ausführung des Programms verheerende Folgen haben konnten.
  • Die Darstellung eines Vorganges als unstrukturierte, lineare, monotone Sequenz von Befehlen ist eine für den Menschen ungeeignete Form, komplizierte Prozesse zu beschreiben und zu überblicken. Die Präsenz von hierarchischen Beschreibungsstrukturen, die eine Sicht auf die Funktionen in unterschiedlicher Detailierungstufe ermöglichen, ist das hauptsächlichste Hilfsmittel, um den Überblick zu wahren und Programme systematisch zu erstellen.

  Diese Unzulänglichkeiten führten unter Anderem zur Entwicklung sogenannter "höherer Programmiersprachen", die zum Einen nach den Gewohnheiten und Fähigkeiten des Menschen im Ausdruck seiner Gedanken ausgerichtet sind und oftmals in ihrer Art und im Umfang am Anwendungsgebiet ausgerichtet sind (und nicht an der unterlegten Hardware).

  Interpreter, Compiler

  Mit den Kommandowörtern der Assemblersprache war ein erster Schritt getan, die Programme für den Menschen verständlich zu schreiben. Man wählte Bezeichnungen, die wie ADD auf die Operation hinwiesen. Doch warum sollte man sich auf Wörter mit drei Buchstaben beschränken? Es wäre noch leichter, Programme zu schreiben, wenn man näher an der Umgangssprache formulieren könnte. Nun wiederholte sich der gleiche Schritt, der von Maschinensprachen zu Assemblersprachen geführt hatte. Man entwickelte (kompliziertere) Übersetzungsprogramme, sie heißen Interpreter und Compiler. Diese neuen Programme übersetzten zunehmend komplexe Buchstabenfolgen in eine Form, die der Computer verstehen kann. Damit konnten die Programme in einer Sprache geschrieben werden, die aus Wörtern der Umgangssprache bestand.

  

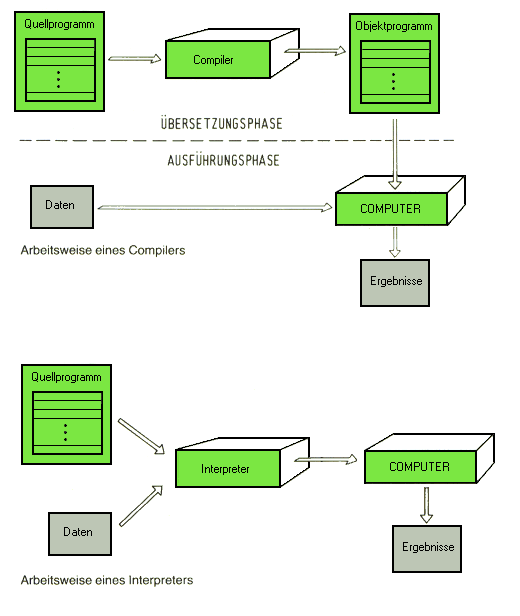
  Meist tun diese Programme noch mehr, als nur zu übersetzen: Es meldet dem Programmierer auch Stellen in seinem Programm, die nicht den Konventionen der Sprache genügen - Programmierfehler also. Ein Maschinenprogramm läßt sich nur noch unter den größten Schwierigkeiten verstehen. Ein Beispiel soll das verdeutlichen:

  a) In natürlicher Sprache: Schreibe das Wort "PASCAL"
  b) In der höheren Sprache C: printf ("PASCAL");
  c) In der Maschinensprache des programmierbaren Taschenrechners TI-59:
  69 00 03 03 01 03 03 06 01 05 01 03 69 01
  02 07 00 00 00 00 00 00 00 00 69 02 69 05
  

  Wie Sie sehen, bieten die höheren Programmiersprachen ganz entscheidende Vorteile. Wir habe also kennengelernt:

  • Assemblersprache (kurz: Assembler, maschinenorientiert) Hier wird jeder Maschinenbefehl durch eine mnemotechnische Abkürzung bezeichnet. Speicheradressen können mit symbolischen Namen versehen werden. Die Zuordnung von Assemblerbefehl zu Maschinenbefehl ist 1:1, d. h. für jeden Maschinenbefehl wird ein Assemblerbefehl benötigt. Die Assemblersprache ist daher extrem stark an den jeweiligen Prozessor gebunden. Ein Transport des Programms auf einen anderen,nicht kompatiblen Prozessor ist nicht möglich.
  • Höhere Programmiersprachen (problemorientiert) Hier wird die Programmierung in einer eigens entwickelten problemorientierten Sprache vorgenommen (algorithmische Sprache). Die Zuordnung der Befehle ist nicht mehr 1:1, ein Befehl in einer höheren Sprache hat in der Regel eine ganze Folge von Maschinenbefehlen als Ergebnis. Der Vorteil einer problemorientierten Sprache liegt auch darin, daß sie maschinenunabhängig ist. Ein Transfer der Programme auf andere Prozessoren ist mit wenig Aufwand möglich.

  Die Programmiersprachen sind in erster Linie dazu da die Lösung einer Aufgabe in computergerechter Form zu formulieren. Die Lösung einer hier betrachteten Aufgabe soll also durch einen Algorithmus dargestellt in einer Programmiersprache beschrieben sein. Wie muß eine solche Programmiersprache (Algorithmische Sprache) nun aufgebaut sein damit sie geeignet ist beliebige Algorithmen darzustellen?

  Zurück

  Inhaltsverzeichnis

  Nächste