Umrechnung zwischen den Stellenwertsystemen
Umwandlung Dezimalsystem  anderes Stellenwertsystem anderes Stellenwertsystem
Die Darstellung als Potenzreihe kann als Polynom zur Basis B aufgefasst werden. 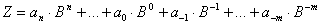 Eine andere Form der Darstellung ist das Hornerschema (hier nur für den ganzzahligen Teil):
Bei der Umwandlung ganzer Zahlen gibt es nur positive Potenzen des Basis B. Bei fortgesetzter Division durch die Basis B' des gesuchten Zahlensystems fallen die gesuchten Koeffizienten als Reste der ganzzahligen Division an. Die Division wird fortgesetzt, bis das Divisionsergebnis 0 geworden ist. Die Divisionsreste sind die Ziffern des Zielsystems in aufsteigender Reihenfolge (1. Rest = niederwertigste Ziffer, letzter Rest = höchstwertige Ziffer). Dezimal-Dual-Wandlung ganzer Zahlen (Basis B = 2) - Dualzahl auf 0 setzen.Wir führen einen Wert I ein, der die gerade bearbeitete
Stelle der erzeugten Dualzahl enthält. I wird auf 1 gesetzt.
- I-te Stelle der Dualzahl := Dezimalzahl mod 2.
(Der Operator "mod" bezeichnet den Rest der Division)
- Dividiere die Dezimalzahl durch 2.
Dieser Wert ergibt die neue Dezimalzahl für die Berechnung
der nächsten Stelle.
- Erhöhe den Wert von I um 1.
Wenn die Dezimalzahl > 0 ist, fahre fort bei Schritt 2.
Dezimal-Dual-Wandlung echtgebrochener Zahlen (Basis B = 2)
Hornerschema für den gebrochenen Teil:
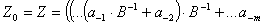
Bei der Umwandlung von echten Brüchen wird nach dem
gleichen Schema verfahren, nur wird hier fortgesetzt mit der Basis
des Zielsystems multipliziert. Die ganzzahligen Anteile der
einzelnen Multiplikationsschritte ergeben die Koeffizienten des
Zielsystems. Die Rechnung ist zuende, wenn der gebrochene Anteil
des Multiplikationsergebnisses 0 wird. Die ganzzahligen Anteile der
Multiplikationen werden dann in absteigender Reihenfolge
aufgeschrieben (1. Anteil = höchste Stelle).
Vorsicht: Ein endlicher Bruch in einem Stellenwertsystem ist nicht immer
auch ein endlicher Bruch in einem anderen.
- Dualzahl auf 0 setzen.
Wir führen einen Wert I ein, der die gerade bearbeitete
Stelle der erzeugten Dualzahl enthält. I wird auf 1 gesetzt.
- Die Dezimalzahl wird mit der Basis 2 multipliziert.
Die I-te Stelle der Dualzahl ergibt sich aus dem ganzzahligen
Anteil der Dezimalzahl (Vorkommastelle).
- Man nehme den gebrochenen Anteil der Dezimalzahl
(Nachkommastellen) für die weitere Berechnungen.
- Man erhöhe den Wert von I um 1.
Wenn die Dezimalzahl > 0 ist, fahre fort bei Schritt 2.
Umwandlung anderes Stellenwertsystem  Dezimalsystem Dezimalsystem
Der offensichtliche Weg ergibt sich aus der Definition einer
Zahl im Stellenwertsystem:
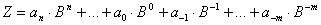
Die Umwandlung erfolgt durch Auswertung der Summe, wobei die
Koeffizienten und die Potenzen der Basis B im Dezimalsystem
dargestellt werden.
Beispiel: Umwandlung aus dem Dualsystem
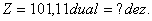
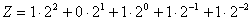
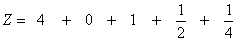
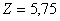
Eine andere Möglichkeit ist wieder die Anwendung des
Hornerschemas. Das oben dargestellte Verfahren der
Dezimal-Dual-Umwandlung wird einfach umgekehrt. Beginnend bei der
höchstwertigen Ziffer wird bei ganzen Zahlen mit der Basis des
Ausgangssystems (dargestellt im Zielsystem) multipliziert und zur
nachfolgenden Stelle addiert. Dies wird bis zur
niederwertigsten Ziffer fortgesetzt. Das letzte Ergebnis ist
die Zahl im Zielsystem.
Dual-Dezimal-Umwandlung, ganzzahlig
- Setze die Dezimalzahl auf 0. Beginne bei der höchstwertigen
Stelle n der Dualzahl.
Wir führen einen Wert I ein, der die gerade bearbeitete
Stelle der erzeugten Dualzahl enthält. I wird auf n gesetzt.
- Multipliziere die Dezimalzahl mit 2 und addiere die I-te Stelle
der Dualzahl zur Dezimalzahl.
- Wiederhole Schritt 2 solange, bis alle Stellen der Dualzahl
verarbeitet sind.
Beispiel: 11011101 dual = ? dezimal
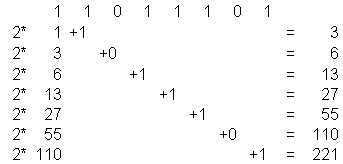
Beispiel: 7C2H = ? dezimal
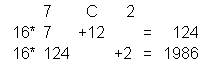
Dual-Dezimal-Umwandlung, echter Bruch
Bei echten Brüchen wird fortgesetzt durch die Basis des
Ausgangssystems (dargestellt im Zielsystem) dividiert. Die Ziffern
werden von der niederwertigsten Stelle aus abgearbeitet (rechts
nach links)  Abbau zum Komma hin. Abbau zum Komma hin.
- Man setze die Dezimalzahl auf 0. Man beginne bei der
niederwertigen Stelle n der Dualzahl.
Wir führen einen Wert I ein, der die gerade bearbeitete
Stelle der erzeugten Dualzahl enthält. I wird auf n gesetzt.
- Man addiere die I-te Stelle der Dualzahl zur Dezimalzahl und
dividiere das Ergebnis durch 2.
- Man wiederhole Schritt 2 solange, bis alle Stellen der Dualzahl
verarbeitet sind.
Beispiel: 0,1011 dual = ? dezimal
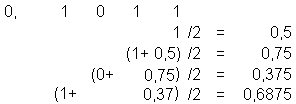
Umwandlung Dual - Oktal - Hexadezimal
Die behandelten Umwandlungsroutinen können hier genauso
verwendet werden. Da die Rechenoperationen immer im Zielsystem
durchgeführt werden, ist dies für uns zumindest
ungewohnt. Es gibt aber ein einfacheres Verfahren, das über
das Dualsystem führt. Alle Basen sind Zweierpotenzen:
- oktal
 3 Dualstellen = 1 Oktalstelle 3 Dualstellen = 1 Oktalstelle
- hexadezimal 4 Dualstellen = 1 Hexadezimalstelle
Die Umwandlung erfolgt in zwei Schritten:
- Umwandlung in das Dualsystem.
Jede Stelle wird in 3 (oktal) oder 4 (hexadezimal) Dualstellen
umgewandelt.
- 3 bzw. 4 Dualstellen werden zusammengefasst und in eine Oktal-
bzw. Hexadezimalstelle gewandelt. Die Dualzahl ist gegebenenfalls
vorher auf volle 3er- oder 4er-Gruppen zu ergänzen (0!). Die
Umwandlung erfolgt immer vom Komma weg (ganzzahliger Anteil nach
links, gebrochener Anteil nach rechts).
Beispiel: oktal 237.54 = ? sedezimal
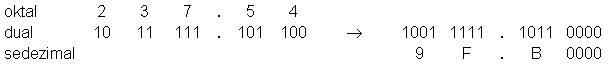
| 
