 |
Stellenwertsysteme
Für den Wert einer Zahl 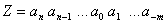 in einem Stellenwertsystem zur Basis B gilt:
in einem Stellenwertsystem zur Basis B gilt: 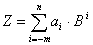 wobei für die Ziffern 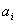 gilt: gilt: 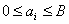 Als Basis bezeichnet man die kleinste, nicht mehr durch eine Ziffer darstellbare Zahl. Am geläufigsten ist uns das Dezimalsystem mit der Basis 10 Die Festlegung ist rein willkürlich und vermutlich auf die Zahl der Finger beider menschlicher Hände zurückzuführen.  Zahlzeichen der Azteken (Basis 20, Ziffernwertsystem), Zahlzeichen der Inkas (Basis 10, Stellenwertsystem). Zahlzeichen der Azteken (Basis 20, Ziffernwertsystem), Zahlzeichen der Inkas (Basis 10, Stellenwertsystem). Die verkürzte Schreibweise durch Aneinanderreihung von Ziffern ist eine abkürzende Schreibweise der Summenformel. Damit kann jede positive und negative reelle Zahl dargestellt werden, indem jede Stelle der Ziffernfolge mit einer Zehnerpotenz gewichtet wird. Ganze Zahlen: 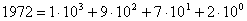 allgemein: 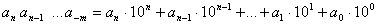 Echter Dezimalbruch:
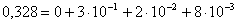
allgemein:
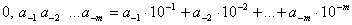
Dezimalzahlen:
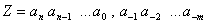 Radixschreibweise
Radixschreibweise
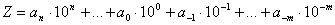 Potenzschreibweise
Potenzschreibweise
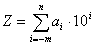 Potenz-Summen-Schreibweise
Potenz-Summen-Schreibweise
Dualzahlen
Prinzipiell kann jede ganze Zahl > 1 Basis B eines
Stellewertsystems sein. Für das Dualsystem ist Basis
B = 2 und a aus {0,1}, z. B. Z = 1010.1 = 10.5 dez. Dieses
Zahlensystem ist speziell für die Digitaltechnik von
Bedeutung, da nur zwei Zustände eine physikalischen
Größe benötigt werden (Spannung, Strom, Frequenz,
Magnetisierungsrichtung).
Nachteil ist die unübersichtliche, monotone Ziffernfolge
bei der Darstellung langer Dualzahlen. Daher werden beim Umgang mit
EDV-Anlagen zwei andere Zahlensysteme verwendet:
Oktalzahlen
Zusammenfassung von 3 Dualstellen zu einer Oktalstelle (bessere
Lesbarkeit, kürzer zu schreiben, leicht umzurechnen)
 Oktalsystem: Basis B = 8 und a ist aus
{0,1,2,3,4,5,6,7}, z. B. 101001 dual = 51 oktal. Oktalsystem: Basis B = 8 und a ist aus
{0,1,2,3,4,5,6,7}, z. B. 101001 dual = 51 oktal.
Bei der Eingabe von Oktalzahlen müssen diese - zur
Unterscheidung von Dezimalzahlen - gekennzeichnet werden. Dies
geschieht durch Hinzustellen der Basis, z. B.:
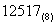
Häufig (besonders bei Programmiersprachen) geschieht dies
auch durch Voranstellen von @ oder Anfügen von O,Q,C z.B.:
@154 154O 154Q 154C (bei C-Compilern auch durch führende Null).
Sedezimalzahlen (= Hexadezimalzahlen)
Zusammenfassung von 4 Dualstellen ergibt eine
Sedezimalstelle  Sedezimalsystem:
Basis B = 16 und a aus {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, z. B.
101001 dual = 29 sedezimal. Übliche Darstellung der
eigentlich binären Information in einem Rechner
(Kurzschreibweise binärer Info). Kennzeichnung bei der
Programmierung durch Voranstellen von $, 0x oder Anfügen von H
z.B.: $FFC2 FFC2H 0xFFC2. Sedezimalsystem:
Basis B = 16 und a aus {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, z. B.
101001 dual = 29 sedezimal. Übliche Darstellung der
eigentlich binären Information in einem Rechner
(Kurzschreibweise binärer Info). Kennzeichnung bei der
Programmierung durch Voranstellen von $, 0x oder Anfügen von H
z.B.: $FFC2 FFC2H 0xFFC2.
Weitere, manchmal verwendete Zahlensysteme, sind das
Ternärsystem (B = 3) und das Quinärsystem
(B = 5). Es stellt sich nun die Frage, wie man Zahlen von
einem Zahlensystem in ein anderes umrechnen kann.
|
|
|

