 |
Arithmetik im Dualsystem
Grundsätzlich wird im Dualsystem nach genau denselben
Regeln gerechnet, wie im Dezimalsystem. Lediglich durch das ungewohnte Zahlensystem erscheint und die Rechner schwieriger zu sein. Arithmetische Grundoperationen Für die Addition zweier einstelliger Dualzahlen S = a + b gilt:
| a | b | S | C | | 0 | 0 | 0 | 0 | | 0 | 1 | 1 | 0 | | 1 | 0 | 1 | 0 |
| 1 |
1 |
0 |
1 |
Bei der letzten Operation entsteht ein Übertrag auf
die folgende Stelle (Carry). Das Ergebnis ist nicht mehr
einstellig darstellbar. Die Addition mehrstelliger Dualzahlen wird
wie im Dezimalsystem stellenweise durchgeführt (Übertrag
berücksichtigen).
Beispiel:
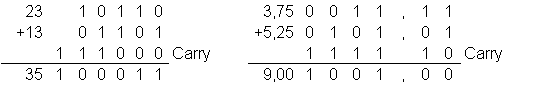
Für die Subtraktion einstelliger Dualzahlen D = a - b gilt:
| a |
b |
D |
B |
| 0 |
0 |
0 |
0 |
| 0 |
1 |
1 |
-1 |
| 1 |
0 |
1 |
0 |
| 1 |
1 |
0 |
0 |
Bei der Operation 0 - 1 ist von der
nächsthöheren Stelle zu "borgen" (Borrow).
Die Subtraktion mehrstelliger Zahlen erfolgt wieder stellenweise.
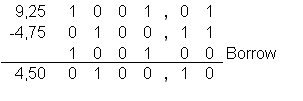
Darstellung negativer Zahlen
Ein sehr einfacher Ansatz wäre es, ein Bit als Vorzeichen
definieren und den Betrag des Zahlenwerts in den restlichen
Bits des Wortes darstellen  Betrags-Vorzeichen-Form. Bei der
technischen Realisierung gibt es jedoch einige Nachteile. In der
Datenverarbeitung ist das Subtraktionsverfahren mit einem
"Borrow"-Signal von der nächsthöheren Stelle
nicht gut durchführbar. Daher führt man die Subtraktion
auf die Addition einer negativen Zahl zurück. Die Darstellung
negativer Zahlen erfolgt durch die sogenannte
Komplementdarstellung. Betrags-Vorzeichen-Form. Bei der
technischen Realisierung gibt es jedoch einige Nachteile. In der
Datenverarbeitung ist das Subtraktionsverfahren mit einem
"Borrow"-Signal von der nächsthöheren Stelle
nicht gut durchführbar. Daher führt man die Subtraktion
auf die Addition einer negativen Zahl zurück. Die Darstellung
negativer Zahlen erfolgt durch die sogenannte
Komplementdarstellung.
Rückführung der Subtraktion auf die Addition:
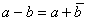 , wobei , wobei 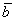 das Komplement von b ist. das Komplement von b ist.
Es stellt sich nun sofort die Frage, wie man das Komplement
einer Zahl erhält. Dazu wird die Gleichung erweitert:
a - b = a + (K - b) - K), wobei K die "Komplementärzahl" ist.
Beispiel:
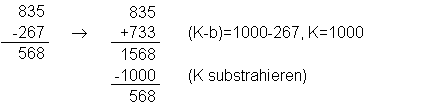
Die Subtraktion von K zum Schluss kann man recht einfach durch
Weglassen der vordersten Stelle beim Ergebnis realisieren.
K ist im Prinzip beliebig wählbar, jedoch würde
für K = 1000 eine Zahl in Komplementdarstellung nicht
von einer natürlichen Zahl unterscheidbar. Wir treffen daher
zwei Vereinbarungen:
- Für alle Rechnungen wird eine maximale Stellenzahl n
festgelegt.
- Für K wird (im Dezimalsystem) 10n+1
gewählt. Dann kann man nämlich eine
Vorzeichenstelle verwenden. Wir vereinbaren:
- Vorzeichenstelle = 0: positive Zahl
- Vorzeichenstelle = 9: negative Zahl
Die Vorzeichenstelle dient zwar als Indikator für das
Vorzeichen, ist jedoch Bestandteil der Zahl!
Beispiele (Komplement mit VZ-Stelle):
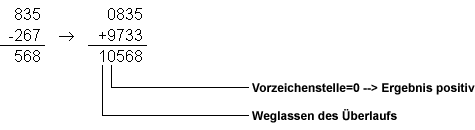

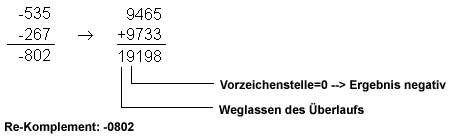
Nun ist also auch ein negatives Ergebnis erkennbar und der
Betrag (bzw. das Endergebnis) kann durch nochmaliges
Komplementieren ermittelt werden.
Interessant wird diese Methode jedoch erst im Dualsystem.
Komplementbildung im Dualsystem
Zunächst eine allgemeine Definition. Es sind zwei Arten von
Komplementen gebräuchlich. X sei eine n-stellige positive Zahl
im Zahlensystem zur Basis B, dann ist:
- B-Komplement (Zweierkomplement):
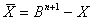
("echtes Komplement")
- (B-1)-Komplement (Einerkomplement):
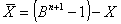
("unechtes Komplement","Stellenkomplement")
Auch hier gilt: Werden alle n Stellen für den Zahlenwert
benutzt, dann ist nicht unterscheidbar, ob eine pos. Zahl oder das
Komplement dargestellt wird  (n+1)-te Stelle hat VZ-Funktion. (n+1)-te Stelle hat VZ-Funktion.
Die Bildung des Einerkomplements geschieht durch Invertieren
jeder einzelnen Stellen (sehr einfach). Es gibt jedoch zwei
"Nullen", für 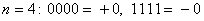 . Vor allem bei EDV-Systemen wird
deshalb das Zweierkomplement verwendet. Die Bildung kann auf zwei
Wegen erfolgen: . Vor allem bei EDV-Systemen wird
deshalb das Zweierkomplement verwendet. Die Bildung kann auf zwei
Wegen erfolgen:
- Einerkomplement bilden und dann 1 addieren:
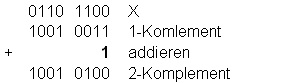
- Direkt: Übernahme aller Stellen von rechts bis zur ersten 1
einschließlich, alle weiteren Stellen invertieren:
 Wertebereich bei n+1 Stellen (n Ziffern und VZ): -2n bis +2n-1
Wertebereich bei n+1 Stellen (n Ziffern und VZ): -2n bis +2n-1
Beispiel: 3 Stellen und Vorzeichen
1000 -8
0111 +7 1001 -7
0110 +6 1010 -6
0101 +5 1011 -5
0100 +4 1100 -4
0011 +3 1101 -3
0010 +2 1110 -2
0001 +1 1111 -1
0000 0
Frage: Warim nicht -2n bis +2n?
Antwort: Der Wert 2n wäre 1000, die Darstellung passt nicht mehr
in 3 Stellen mit Vorzeichen  Verwechselung mit -8! Verwechselung mit -8!
Die Gesamtheit der so dargestellten Zahlen nennt man
konegative Zahlen (gesprochen "konegativ", kommt
von "Komplement-negativ"). Der Vorteil der
Komplementdarstellung von negativen Zahlen liegt in der
Ausführbarkeit der Subtraktion als Addition.
B-Komplement:
Y - X = Y - (X + Bn) - Bn = Y + X - Bn
Bn = 1000...000 (n Nullen)
Beispiele für die Komplement-Bildung
(Basis = 2, Stellenzahl n = 4  3 Ziffern und VZ) 3 Ziffern und VZ)
Dez. Dual 1-kompl. 2-kompl.
0 0000 1111 0000
2 0010 1101 1110
5 0101 1010 1011
7 0111 1000 1001
Bei der Subtraktion wird das Komplement addiert und (bei pos.
Ergebnis) der Übertrag in die n+1-te Stelle
weggelassen. Bei negativem Ergebnis: Komplementdarstellung.
Das Carry-Bit (Übertrag) wird gesetzt, wenn in der
höchstwertigen Stelle ein Übertrag auftritt.
Wemm man bei dem oben angegebenen Zahlenbereich 5 + 7 addiert,
ergibt sich folgende Rechnung:
0101
0111
----
1100
Das Ergebnis 1100 ist eindeutig negativ, nämlich -4. Es liegt
nicht im darstellbaren Zahlenbereich! Untersucht man die verschiedenen
Möglichkeiten unf fasst man die Erkenntnisse zusammen, ergibt sich
folgende Tabelle:
Vorzeichen
Operanden |
Vorzeichen
Ergebnis |
Bereichs-
überschr. |
|
beide
positiv |
positiv
negativ |
nein
ja |
!! |
positiv
negativ |
positiv
negativ |
nein
nein |
|
beide
negativ |
positiv
negativ |
ja
nein |
!! |
Merksatz:
Wenn beide Operanden das gleiche Vorzeichen haben und das
Ergebnis ein davon abweichendes Vorzeichen, dann gab es eine
Bereichsüberschreitung (Overflow).
Die bisher gesammelten Erkenntnisse führen dann zur
Rechenvorschrift für die Subtraktion durch Komplementaddition
(B-Komplement):
- Stellenzahl von X und Y angleichen
- B-Komplement Xk des Subtrahenden X bilden
- Y und Xk addieren
- Eventuellen Übertrag streichen
- Ist VZ-Stelle von Y = VZ-Stelle von X und unterscheidet
sie sich von der VZ-Stelle des Ergebnisses, dann ist ein
Zahlenbereichsüberlauf aufgetreten
 Fehlermeldung. Fehlermeldung.
- Ist die VZ-Stelle des Ergebnisses = 0, dann ist das Ergebnis
positiv, sonst ist das Ergebnis negativ (in
B-Komplement-Darstellung). Will man in diesem Fall den Betrag des
Ergebnisses feststellen, muss man das Ergebnis komplementieren.
Multiplikation
Bei Multiplikation und Division werden selten konegative Zahlen
verwendet. Es werden vielmehr die Beträge multipliziert und
dann das Vorzeichen betrachtet. Die duale Multiplikation erfolgt
prinzipiell nach den selben Regeln, wie wir sie in der Schule
für das Dezimalsystem gelernt haben: Der Multiplikand wird
stellenweise mit dem Multiplikator malgenommen und die so
erhaltenen Teilergebnisse stellenrichtig aufaddiert. Für
Dualzahlen ist die Bestimmung eines Teilergebnisses besonders
einfach. Da an der Multiplikatorstelle nur die Werte 0 oder 1
stehen können, ist bei einer 0 das Teilergebnis auch 0, im
Fall der 1 ist das Teilergebnis identisch mit dem
Multiplikanden.
Beispiel: 23 * 12 = 276
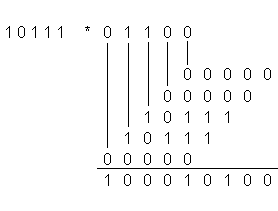
Das Ergebnis zweier n-stelliger Dualzahlen hat nahezu die
doppelte Stellenzahl, nämlich 2n - 1.
Die Multiplikation von Dualzahlen kann durch Addition und
Bitverschiebung vereinfacht werden ( Verschieben um eine
Bitposition entspricht Multiplikation mit 2 (links) oder Division
durch 2 (rechts). Alle Rechenanlagen besitzen
Bit-Verschiebe-Befehle. Angefangen bei niederwertigsten Bit des
Multiplikators wird fortlaufend der Multiplikand zum
Ergebnisregister (das zu Beginn auf Null gesetzt wurde) addiert,
wenn das entsprechende Bit des Multiplikators den Wert 1 besitzt
und dann um eine Position nach links verschoben. Die
stellenrichtige Addition wird also nur in Teilschritte zerlegt.
Beispiel: 9 * 13 = 117
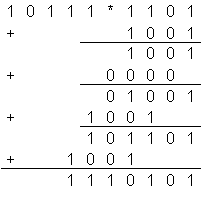
Algorithmus für X * Y:
- Setze Ergebnisspeicher auf 0
- wenn die letzte Stelle von Y = 1 ist, addiere X zum
Ergebnisspeicher
- Verschiebe Y um eine Stelle nach rechts (die in Schritt
1. behandelte Stelle wird "hinausgeschoben", sie verschwindet also).
- Verschiebe X um eine Stelle nach links (entspricht
Multiplikation mit 2
 stellenrichtige Addition) stellenrichtige Addition)
- Wenn Y nicht 0 ist, gehe zu Schritt 2.
Die 5. Anweisung hat zur Folge, dass die Multiplikation beendet
wird, sobald nichts mehr zu addieren ist. Bei einer Wortbreite von
n, ist die Multiplikation auf jeden Fall nach n
Schritten zuende.
Division
Auch bei der Division X/Y wird nur Addition, Subtraktion
(= Komplementaddition) und das Multiplizieren/Dividieren mit 2
benötigt. Zunächst wird Y in einem Hilfsregister
W gespeichert und W dann solange nach links
verschoben (also verdoppelt), bis W > X ist. Der
Divisionsrest R erhält den Wert von X. Danach wird
fortlaufend W durch 2 dividiert und der Quotient mit 2
multipliziert, bis W = X ist. Wenn dabei W kleiner
als der Rest wird, dann wird W vom Rest abgezogen und Q
erhöht (Korrektur).
Beispiel im Dezimalsystem: 651 / 5
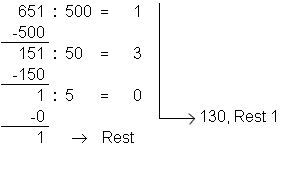
Algorithmus für X / Y:
- Setze Quotient auf 0. Setze Rest = X. Setze
Zwischenspeicher W = Y.
- Verdopple W solange, bis W > Rest ("wie
oft geht Y in X")
- Wenn W = Y ist, dann ist die Division zuende.
- Verdopple den Quotientenwert (Q := Q * 2). Halbiere W
(W = W / 2).
- Wenn W <= Rest dann subtrahiere W vom Rest und
Erhöhe den Quotienten um 1.
- Fahre fort bei Schritt 3.
Der Trick hinter diesem Algorithmus ist die Gleichung
X = Quotient * W + Rest
Die Gleichung ist nach jedem Durchlauf der Rechenschritte 3. bis
6. erfüllt.
Beispiel:

Ergebnis: Q(uotient) = 100, R(est) = 10
|
| |

