 |
Festpunkt- und Gleitpunktdarstellung
Festpunktzahlen
Die bisher betrachtete Schreibweise gebrochener Zahlen wird Festpunktdarstellung (Festkommadarstellung) genannt. Bei einer vorgegebenen Gesamtstellenzahl steht der Radixpunkt immer an der gleichen Stelle. Wie weit die erste von Null verschiedenen Ziffer vom Punkt entfernt steht, hängt von der Größe der Zahl ab, z. B. Darstellung mit Vorzeichen, 8 Stellen vor dem Komma und 3 Stellen dahinter (dezimal). 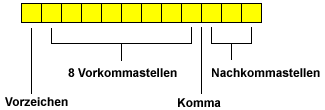 Die Zahl wird mit führenden Nullen dargestellt und gegebenenfalls gerundet. Im obigen Beispiel reicht der darstellbare Bereich von -99999999,999 bis +99999999,999. Der Nachteil liegt im begrenzten Zahlenbereich  bei sehr kleinen Zahlen gehen durch die Rundung Stellen verloren (0,0009 würde z. B. zu 0), sehr große Zahlen sind nicht mehr darstellbar. Gleitpunktzahlen Gebrochene Zahlen (reelle Zahlen) werden i.a. inGleitpunktdarstellung (Gleikomma-Darst.) bearbeitet. Gleitpunktzahlen, floating point numbers). Wegen der endlichen Stellenzahl können reelle Zahlen nur unvollkommen dargestellt werden, sie repräsentieren nur einzelne Punkte auf der reellen Zahlengerade Rundungsfehler. Bei der Gleitpunktdarstellung wird die Zahl so gespeichert, daß der Radixpunkt immer zur ersten von Null verschiedenen Ziffer gleitet. Dieserreicht man durch Abspalten einer entsprechenden Potenz der Basis:
Z = M * BE, n ganzzahlig
M = 0.xxxxxxx..., 1/B <= M < 1
Da die Basis bekannt ist, kann die Zahl durch die Mantisse M und
den Exponenten E dargestellt werden. halblogarithmische
Darstellung normalisierte Darstellung. Die Anpassung der
GP-Zahl an die angegebene Darstellungsform wird als
"Normalisieren" bezeichnet.
Beispiel:
Z = 42.5456 0.425456 * 102
M = 425456, E = 2
Man bezeichnet E als Exponent (bzw. Charakteristik)
Größenordnung der Zahl und M als
Mantisse Angabe der gültigen Zifferndarstellungen
Die Art der Darstellung von Mantisse und Exponent ist recht
unterschiedlich. Für Mantisse und Exponent wird jeweils eine
feste Stellenzahl vorgegeben, in der auch das Vorzeichen von
Mantisse und Exponent untergebracht werden muss. Am üblichsten
ist Betrags-Vorzeichen-Darstellung der Mantisse und
Exponentendarstellung mit verschobenem Wertebereich
(Charakteristik) so, dass der Wert der Charakteristik immer ³
0 ist (so wird ein zusätzliches Bit für das Vorzeichen
des Exponenten eingespart). Sie stellt also eine einfache
Verschiebung des Wertebereichs dar und hat keinen Einfluss auf die
Berechnung.
Beispiel:
Wertebereich Exponent: -128 ... 127
Charakteristik (C = E + V): 0 ... 255 (V = 128)
Umwandlung einer Dezimalzahl in eine Gleitpunkt-Dualzahl:
1. Methode:
- Getrennte Umwandlung des ganzahligen und gebrochenen Anteils
- Verschieben des Radixpunktes bis zur ersten von Null
verschiedenen Ziffer (Normalisierung).
Beispiel: (8 Stellen Mantisse, 4 Stellen Exponent, V = 8)
27.75 dez. = 11011.11 dual M = 0.1101111, E = 0101
M = 0.1101111, C = 1101
2. Methode:
- Abspalten der nächstgrößeren Zweierpotenz (d.h.
dividieren durch 2, bis das Ergebnis kleiner 1 ist)
- Getrennte Umwandlung von Mantisse (echter Bruch) und Exponent
(ganzzahlig).
Beispiel: (8 Stellen Mantisse, 4 Stellen Exponent, V = 8)
27.75 dez. M = 0.8671875, E = 5
M = 0.1101111, E = 0101
M = 0.1101111, C = 1101
Eigenschaften von Gleitpunktzahlen:
- Die Gleitkommadarstellung ist immer auf eine bestimmte Zahl von
Stellen genau (die Anzahl der Mantissenstellen) bestimmte
relative Genauigkeit, z.B. 32-Bit-Mantisse (einschl. VZ) 31
Dualst. 9 Dezimalstellen. Reelle Zahlen werden also immer auf
die nächstgelegene GK-Zahl gerundet.
- Die Gleitkommadarstellung hat den Vorteil, daß man mit bestimmter
Stellenzahl einen viel größeren Zahlenbereich darstellen
kann, als mit Fixkommazahlen.
- Manchmal wird auch eine Darstellung verwendet, bei welcher der
Radixpunkt rechts der ersten von Null verschiedenen Ziffer steht
(z.B. 1.100101). Im Dualsystem ist diese Ziffer immer 1 und kann
deshalb bei der Speicherung in EDV-Systemen weggelassen werden
(impliziter ganzer Teil der Mantisse).
Gleitpunkt-Arithmetik
Auch hier gilt wieder, dass die Rechenverfahren verwendet
werden, die wir in der Schule gelernt haben - eben nur angewendet
auf Dualzahlen.
Addition und Subtraktion:
- Angleichen der Exponenten der beiden Operanden (Verschieben der
Mantisse des Operanden mit kleineren Exponenten)
- Addition/Subtraktion der Mantissen
- Normalisieren des Ergebnisses
Multiplikation und Division:
- Multiplikation/ Division der Mantissen
- Addition/ Subtraktion der Exponenten
- Normalisieren des Ergebnisses
Beispiel für Gleitpunkt-Addition im Dualsystem:
(6 Stellen Mantisse, 4 Stellen Charakteristik)
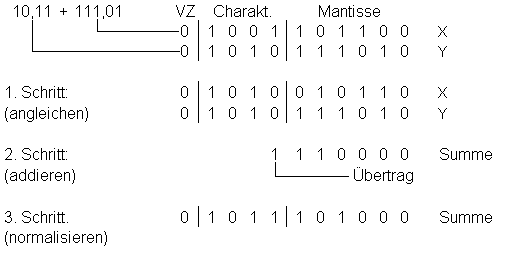
Assoziativität und Distributivität gilt nicht mehr
Durch die begrenzte Stellenzahl entstehen u. U. Rundungsfehler
beim Angleichen der Operanden (Rundungsfehler). Das
Assoziativgesetz und das Distributivgesetz gelten nicht mehr.
a + (b + c) ungleich (a + b) + c
a * (b * c) ungleich (a * b) * c
(a + b) * c ungleich (a * c) + (b * c)
Einfaches Beispiel:
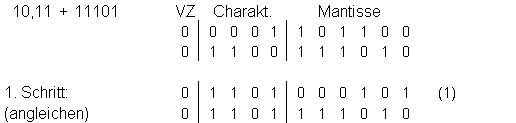
Beim Angleichen geht die letzte Stelle des ersten Summanden verloren.
Beispiel für Gleitpunkt-Formate
Bei EDV-Anlagen mit großer Maschinenwortlänge werden
Mantisse und Exponent meist in einem Maschinenwort untergebracht.
Die GK-Arithmetik wird meist von der Hardware unterstützt. Bei
Mikrocomputern ist die GK-Arithmetik meist durch Software
realisiert (Ausnahme: spezielle GK-Koprozessoren). Häufig wird
neben einen Format für einfache Genauigkeit ein weiteres
Format für erweiterte Genauigkeit angeboten.
Beispiel: DIN IEC 47B für Mikroprozessoren
|
|
|
DIENSTE
